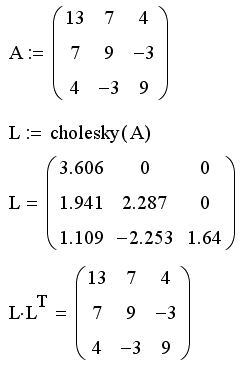Матричные разложения. Разложение Холецкого.
Современная вычислительная линейная алгебра – бурно развивающаяся наука. Главная проблема, рассматриваемая ею, – это проблема решения систем линейных уравнений. В настоящее время разработано множество методов, упрощающих эту задачу, которые, в частности, зависят от структуры матрицы СЛАУ.
Большинство методов основано на представлении матрицы в виде произведения других матриц специального вида или матричных разложениях. Как правило, после определенного разложения матрицы задача линейной алгебры существенно упрощается. В Mathcad имеется несколько встроенных функций, реализующих алгоритмы наиболее популярных матричных разложений.
Разложением Холецкого симметричной матрицы А является представление вида A=L LT, где L – треугольная матрица (т. е. матрица, по одну из сторон от диагонали которой находятся одни нули). Алгоритм Холецкого реализован во встроено функции сholesky.
- cholesky (А) – разложение Холецкого;
- А – квадратная, положительно-определенная матрица.
Пример разложения Холецкого приведен в листинге 9.40. Обратите внимание, что в результате получается верхняя треугольная матрица (нули сверху от диагонали), а транспонированная матрица является нижней треугольной. В последней строке листинга приведена проверка правильности найденного разложения.
Листинг 9.40. Разложение Холецкого: