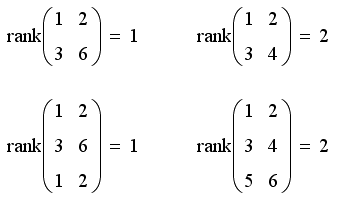Число обусловленности квадратной матрицы. Ранг матрицы.
Еще одной важной характеристикой матрицы является ее число обусловленности (condition number). Число обусловленности является мерой чувствительности системы линейных уравнений Ах=b, определяемой матрицей А, к погрешностям задания вектора b правых частей уравнений. Чем больше число обусловленности, тем сильнее это воздействие и тем более неустойчив процесс нахождения решения. Число обусловленности связано с нормой матрицы и вычисляется по-разному для каждой из норм;
- cond1 (A) – число обусловленности в норме L1;
- cond2 (A) – число обусловленности в норме L2;
- conde (A) – число обусловленности в евклидовой норме;
- condi (A) – число обусловленности в норме;
- А – квадратная матрица.
Расчет чисел обусловленности для двух матриц А и В показан в листинге 9.31. Обратите взимание, что первая из матриц является хорошо обусловленной, а вторая – плохо обусловленной (две ее строки определяют очень близкие системы уравнений, с точностью до множителя з). Вторая строка листинга дает формальное определение числа обусловленности как произведения норм исходной и обратной матриц. В других нормах определение точно такое же.
Как нетрудно понять, матрицы А и в из предыдущего листинга 9.30 обладают одинаковыми числами обусловленности, т, к. В=100А, и, следовательно, обе матрицы определяют одну и ту же систему уравнений.
Листинг 9.31. Числа обусловленности матриц:
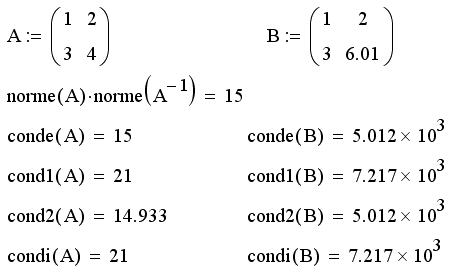
Ранг матрицы
Рангом (rank) матрицы называют наибольшее натуральное число k, для которого существует не равный нулю определитель k-ro порядка подматрицы, составленной из любого пересечения k столбцов и k строк матрицы.
Для вычисления ранга в Mathcad предназначена функция rank.
- rank (А) – ранг матрицы;
- А – матрица.
Листинг 9.32. Ранг матрицы: