Норма квадратной матрицы
В линейной алгебре используются различные матричные нормы (norm), которые ставят в соответствие матрице некоторую скалярную числовую характеристику. Норма матрицы отражает порядок величины матричных элементов. В разных специфических задачах линейной алгебры применяются различные виды норм. Mathcad имеет четыре встроенные функции для расчета разных норм квадратных матриц:
- norm1 (A) – норма в пространстве L1;
- norm2 (A) – норма в пространстве L2;
- norme (A) – евклидова норма (euclidean norm);
- normi (A) – max-норма, или норма (infinity norm);
- А – квадратная матрица.
Примеры расчета различных норм двух матриц А и в с различающимися на два порядка элементам! приведены в листинге 9.30. В последней строке этого листинга пояснен) определение евклидовой нормы, которое похоже на определение длины вектора.
Листинг 9.30. Нормы матриц:
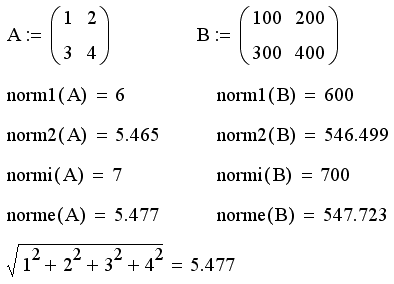
В большинстве задач неважно, какую норму использовать. Как видно, в обычных случаях разные нормы дают примерно одинаковые значения, хорошо отражая порядок величины матричных элементов. Определение остальных норм заинтересованный метатель отыщет в справочниках по линейной алгебре или в справочной системе Mathcad (раздел Mathcad Resources).
