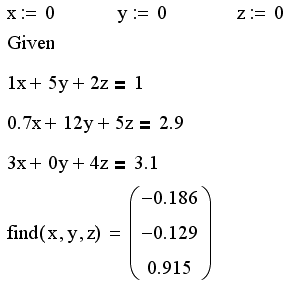Системы линейных алгебраических уравнений
Центральным вопросом вычислительной линейной алгебры является решение систем линейных алгебраических уравнений (СЛАУ), т. е. систем уравнений вида:
аi1X1+аi2х2+…+ainхn=bi (1)
В матричной форме СЛАУ записывается в эквивалентном виде:
Ax = b, (2)Где А – матрица коэффициентов СЛАУ размерности NXN, х – вектор неизвестных, b– вектор правых частей уравнений.
К системам линейных уравнений сводится множество, если не сказать большинство, задач вычислительной математики. Один из таких примеров приведен в разд. "Разностные схемы для ОДУ" гл. 12.
СЛАУ имеет единственное решение, если матрица А является невырожденной, или, по-другому, несингулярной, т. е. ее определитель не равен нулю. С вычислительной точки зрения, решение СЛАУ не представляет трудностей, если матрица А не очень велика. С большой матрицей проблем также не возникнет, если она не очень плохо обусловлена. В Mathcad СЛАУ можно решить как в более наглядной форме (1), так и в более удобной для записи форме (2). Для первого способа следует использовать вычислительный блок Given/Find (см. гл. 8), а для второго – встроенную функцию lsoive.
- lsoive (А, b) – решение системы линейных уравнений;
- А – матрица коэффициентов системы;
- b – вектор правых частей.
Применение функции lsoive показано в листинге 9.33. При этом матрица А может быть определена любым из способов (см. разд. "Массивы" гл. 4), необязательно явно, как во всех примерах этого раздела. Встроенную функцию lsoive допускается применять и при символьном решении СЛАУ (листинг 9.34).
Соответствующая матрице А и вектору b система уравнений выписана явно в листинге 9.35.
Листинг 9.33. Решение СЛАУ:
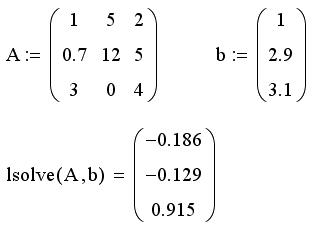
Листинг 9.34. Символьное решение СЛАУ (продолжение листинга 9.33):
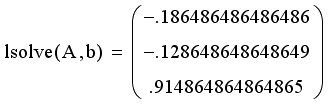
В некоторых случаях, для большей наглядности представления СЛАУ, его можно решить точно так же, как систему нелинейных уравнений (см. гл. 8). Пример численного решения СЛАУ из предыдущих листингов показан в листинге 9.35. Не забывайте, что при численном решении всем неизвестным требуется присвоить начальные значения (это сделано в первой строке листинга 9.35). Они могут быть произвольными, т. к. решение СЛАУ с невырожденной матрицей единственно.
При решении СЛАУ с помощью функции Find Mathcad автоматически выбирает линейный численный алгоритм, в чем можно убедиться, вызывая на имени Find контекстное меню.
Листинг 9.35. Решение СЛАУ с помощью вычислительного блока:
