Вычислительный блок Given/Odesolve
Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутты, состоит из трех частей:
- Given – ключевое слово;
- ОДУ и начальное условие, записанное с помощью логических операторов, причем начальное условие должно быть в форме у (t1) = b;
- odesoive(t, t1) – встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1).
Допустимо, и даже часто предпочтительнее, задание функции Odesolve (t, t1, step) с тремя параметрами, где step– внутренний параметр численного метода, определяющий количество шагов, в которых метод Рунге-Купы, будет рассчитывать решение дифференциального уравнения. Чем больше step, тем с лучшей точностью будет получен результат, но тем больше времени будет затрачено на его поиск. Помните, что подбором этого параметра можно заметно (в несколько раз) ускорить расчеты без существенного ухудшения их точности.
Пример решения задачи Коши для ОДУ первого порядка у' =у-у2 посредством вычислительного блока приведен в листинге 11.1.
Листинг 11.1. Решение задачи Коши для ОДУ первого порядка:
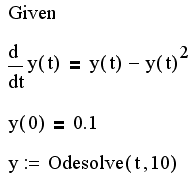
Не забывайте о том, что вставлять логические операторы следует при помощи панели инструментов Boolean (Булевы операторы). При вводе с клавиатуры помните, что логическому знаку равенства соответствует сочетание клавиш CTRL + =. Символ производной можно ввести как средствами панели Calculus (Вычисления), как это сделано в листинге 11.1, так и в виде штриха, набрав его с помощью сочетания клавиш CTRL + F7 (соответствующий пример будет приведен ниже в листинге 11.3.) Выбирайте тот или иной способ представления производной из соображений наглядности представления результатов – на ход расчетов он не влияет.
Mathcad требует, чтобы конечная точка интегрирования ОДУ лежала правее начальной: t0<t1 (в листинге 11.1 t0=0,t1=10), иначе будет выдано сообщение об ошибке. Как можно заметить, результатом применения блока Given/odesoive является функция y(t), определенная на промежутке (t0,t1). Следует воспользоваться обычными средствами Mathcad, чтобы построить ее график или получить значение функции в какой-либо точке указанного интервала, например: у(3)=0.691.
Пользователь имеет возможность выбирать между двумя модификациями численного метода Рунге-Кутты. Для смены метода необходимо нажатием правой кнопки мыши на области функции odesolve вызвать контекстное меню и выбрать в нем один из двух пунктов: Fixed (Фиксированный шаг) или Adaptive (Адаптивный). По умолчанию применяется первый из них, т. е. метод Рунге-Кутты с фиксированным шагом.
Подробнее о различии этих методов сказано в разд. 11.3.