Иллюстрированный самоучитель по MathCAD 11

Встроенные функции для решения систем ОДУ

В Mathcad 11 имеются три встроенные функции, которые позволяют решать поставленную в форме (2-3) задачу Коши различными численными методами.

• rkfixed(y0, t0, t1, M, D) – метод Рунге-Кутты с фиксированным шагом,
• Rkadapt(y0, t0, t1, M, D) – метод Рунге-Кутты с переменным шагом;
• Buistoer(y0, t0, t1, M, D) – метод Булирша-Штера;
  • у0 – вектор начальных значений в точке t0 размера NXI;
  • t0 – начальная точка расчета,
  • t1 – конечная точка расчета,
  • M – число шагов, на которых численный метод находит решение;
  • D – векторная функция размера NXI двух аргументов – скалярного t и векторного у. При этом у – искомая векторная функция аргумента t того же размера NXI.

Соблюдайте регистр первой буквы рассматриваемых функций, поскольку это влияет на выбор алгоритма счета, в отличие от многих других встроенных функций Mathcad, например Find=fmd (см разд 11.3.2)

Каждая из приведенных функций выдает решение в виде матрицы размера (M+1)х(N+1). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных N столбцах – значения искомых функций y₀(t),y₁(t),.., y_N-1(t), рассчитанные для этих значений аргумента Поскольку всего точек (помимо начальной) м, то строк в матрице решения будет всего M+1.

В подавляющем большинстве случаев достаточно использовать первую функцию rkfixed, как это показано в листинге 11.4 на примере решения системы ОДУ модели осциллятора с затуханием (см. разд. 11 2).

Листинг 11.4. Решение системы двух ОДУ:

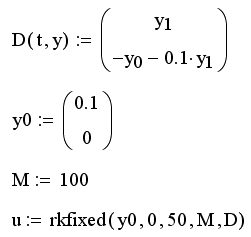
Самая важная – это первая строка листинга, в которой, собственно, определяется система ОДУ. Сравните рассматриваемую систему (разд. 11.2.1), записанную в стандартной форме, с формальной ее записью в Mathcad, чтобы не делать впоследствии ошибок. Во-первых, функция D, входящая в число параметров встроенных функций для решения ОДУ, должна быть функцией обязательно двух аргументов. Во-вторых, второй ее аргумент должен быть вектором того же размера, что и сама функция D. В-третьих, точно такой же размер должен быть и у вектора начальных значений у0 (он определен во второй строке листинга).

Не забывайте, что векторную функцию D(t,y) следует определять через компоненты вектора у с помощью кнопки нижнего индекса (Subscript) с наборной панели Calculator (Калькулятор) или нажатием клавиши [. В третьей строке листинга определено число шагов, на которых рассчитывается решение, а его последняя строка присваивает матричной переменной и результат действия функции rkfixed. Решение системы ОДУ будет осуществлено на промежутке (0, 50).

Как выглядит все решение, показано на рис. 11.3. Размер полученной матрицы будет равен (M+DX(N+I), т.е. Ю1хз. Просмотреть все компоненты матрицы и, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки. Как нетрудно сообразить, на этом рисунке отмечено выделением расчетное значение первого искомого вектора у0 на 12-м шаге u12.1=0.01. Это соответствует, с математической точки зрения, найденному значению У0(6.0)=0.07. Для вывода элементов решения в последней точке интервала используйте выражения типа Uм1=7.523x103.

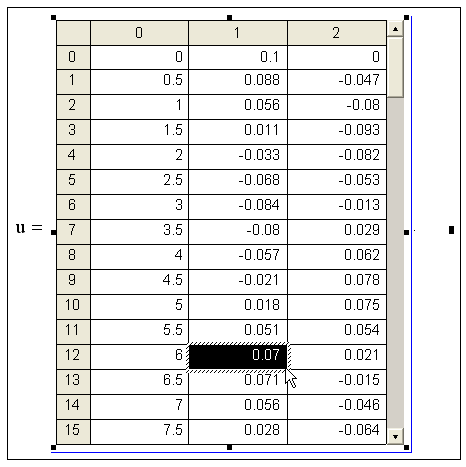
Рис. 11.3. Матрица решений системы уравнений (листинг 11.4)