Иллюстрированный самоучитель по MathCAD 11

ОДУ высшего порядка

Обыкновенное дифференциальное уравнение с неизвестной функцией y(t), в которое входят производные этой функции вплоть до y^(N) (t), называется ОДУ N-го порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши требуется задать N начальных условий на саму функцию y(t) и ее производные от первого до (N-1) го порядка включительно. В Mathcad 11 можно решать ОДУ высших порядков как с помощью вычислительного блока Given/odesolve, так и путем сведения их к системам уравнений первого порядка.

Внутри вычислительного блока:

• ОДУ должно быть линейно относительно старшей производной, т. е. фактически должно быть поставлено в стандартной форме;
• начальные условия должны иметь форму y(t)=b или y^(N) (t)=b, а не более сложную (как, например, встречающаяся в некоторых математических приложениях форма у (t) +у' (t) = b)

В остальном, решение ОДУ высших порядков ничем не отличается от решения уравнений первого порядка (см. разд. 11.1), что иллюстрируется листингом 11.3. Как Вы помните, допустимо написание производной как в виде знака дифференциала (так в листинге 11.3 введено само уравнение), так и с помощью штриха (так введено начальное условие для первой производной). Не забывайте пользоваться булевыми операторами при вводе уравнений и начальных условий.

Листинг 11.3. Решение задачи Коши для ОДУ второго порядка:

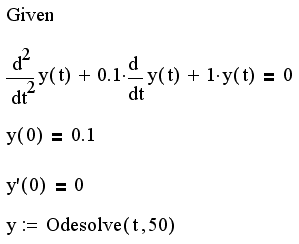
Полученное решение y(t) показано на рис. 11.2.

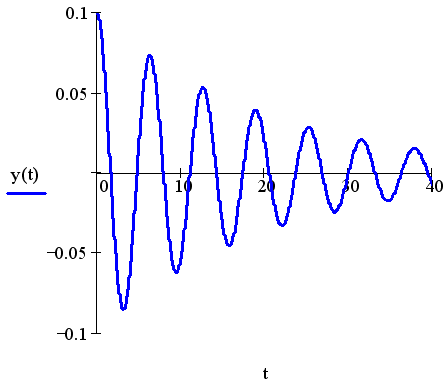
Рис. 11.2. Решение уравнения осциллятора (листинг 11.3)

В листинге 11.3 решено уравнение затухающего гармонического осциллятора, которое описывает, например, колебания маятника. Для модели маятника y(t) описывает изменения угла его отклонения от вертикали, y'(t) – угловую скорость маятника, y"(t) – ускорение, а начальные условия, соответственно, начальное отклонение маятника у (0) =0.1 и начальную скорость у' (0)= 0.

Второй способ решения ОДУ высшего порядка связан со сведением его к эквивалентной системе ОДУ первого порядка. Покажем на том же примере из листинга 11.3, как это делается. Действительно, если формально обозначить y0(t)sy(t), а yi(t)sy'(t)=y0'(t), то исходное уравнение запишется через функции y₀(t) и y₁(t) в виде системы двух ОДУ:

Именно эта система решается в качестве примера в разд. 11.3. Таким образом, любое ОДУ N-го порядка, линейное относительно высшей производной, можно свести к эквивалентной системе N дифференциальных уравнений.