Функции для решения жестких ОДУ
Решение жестких систем дифференциальных уравнений можно осуществить только с помощью встроенных функций, аналогичных по действию семейству рассмотренных выше функций для обычных ОДУ.
- Radau(y0,t0,t1,M,F) – алгоритм RADAUS для жестких систем ОДУ;
- stiffb(y0,t0,t1,M,F,j) – алгоритм Булирша-Штера для жестких систем ОДУ;
- stiffr(y0,t0,t1,M,F,j) – алгоритм Розенброка для жестких систем ОДУ;
- у0 – вектор начальных значений в точке to;
- t0.t1 – начальная и конечная точки расчета;
- M– число шагов численного метода;
- F – векторная функция F(t,y) размера IXN, задающая систему ОДУ;
- J – матричная функция J(t,y) размера (N+DXN, составленная из вектора производных функции F(t,y) no t (правый столбец) и ее якобиана (N левых столбцов).
Как Вы можете заметить, для двух последних функций серьезным отличием от функций, решающих нежесткие системы, является добавление к стандартному набору параметров дополнительной матричной функции, задающей якобиан системы ОДУ. Решение выдается в виде матрицы, по форме идентичной аналогичным функциям решения нежестких задач Коши.
Покажем действие этих алгоритмов на том же примере жесткой системы ОДУ химической кинетики (листинг 11.14). Обратите внимание, как следует представлять в данном случае якобиан, сравнив задание матричной функции в предпоследней строке листинга 11.14 с заданием якобиана из листинга 11.13.
Листинг 11.14. Решение жесткой системы ОДУ химической кинетики:
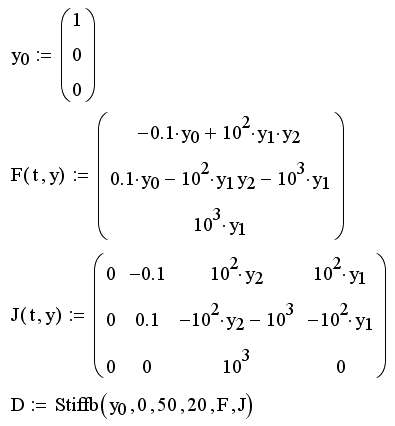
Расчеты показывают, что для получения того же результата (см. рис. 11.18) оказалось достаточно в тысячу раз меньшего количества шагов численного алгоритма, чем для стандартного метода Рунге-Кутты! Примерно во столько же раз требуется меньше компьютерного времени на проведение расчетов. Стоит ли говорить, что, если Вы имеете дело с жесткими (в той или иной степени) системами, применение описанных специальных алгоритмов просто необходимо.
Важно заметить, что до сих пор мы имели дело с примером не очень жесткой системы. Попробуйте вместо скоростей упомянутых химических реакций (см. разд. 11.5.1), 0.1, 103 и 102 взять другие числа, например 0.05, 10 и 107, соответственно. Заметим, что такое соотношение скоростей часто встречается в прикладных задачах химической кинетики и определяет куда более жесткую систему ОДУ. Ее уже никак не удается решить стандартными методами, поскольку число шагов численного метода должно быть просто гигантским. А между тем, алгоритмы для жестких ОДУ справляются с этой задачей с легкостью (рис. 11.19), причем практически при тех же значениях шага, что были взяты в листинге 11.14. Обратите внимание, что порядки величины решений для концентраций различных веществ на рис. 11.19 различаются еще сильнее, чем в предыдущем (менее жестком) примере.
Это еще раз доказывает, что одна и та же система ОДУ с различными коэффициентами может быть жесткой в разной степени. В частности, приведенный выше пример генератора Ван дер Поля с параметром ц=5000 – это уже пример жесткой задачи.
В заключение приведем соответствующие встроенные функции, которые применяются для решения жестких систем ОДУ не на всем интервале, а только в одной заданной точке t1.
- radau(y0, t0, t1,acc,F,k,s) – метод RADAUS
- stiffb(y0,t0,t1,acc,F,j,k,s) – метод Булирша-Штера
- stiffr(y0,t0,t1,acc,F,j,k,s) – метод Розенброка
Имена этих функций пишутся с маленькой буквы, а их действие и набор параметров полностью аналогичны рассмотренным нами ранее для функций, относящихся к решению в заданной точке нежестких систем (см. разд. 11.3.2). Отличие заключается в специфике применяемого алгоритма и необходимости задания матричной функции якобиана j(t,y).
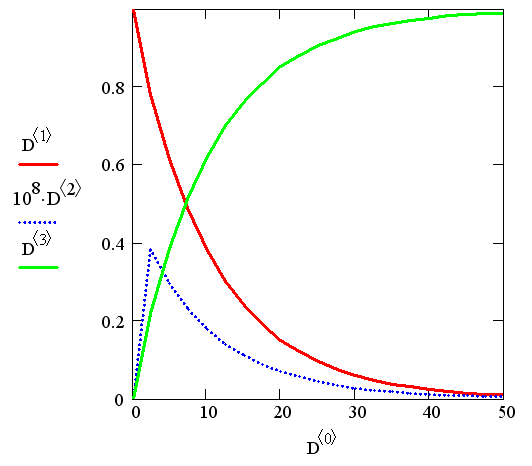
Рис. 11.19. Решение более жесткой системы ОДУ химической кинетики методом Розенброка