Фазовый портрет динамической системы
Для того чтобы поменять количество траекторий, измените соответствующим образом размер этой матрицы. Затем (рис. 11.14) элементы матрицы и выводятся на график в виде отдельных точек. Отсутствие соединения точек линиями является недостатком алгоритма, но это плата за возможность представить в Mathcad несложным образом сразу большое количество траекторий на фазовой плоскости.
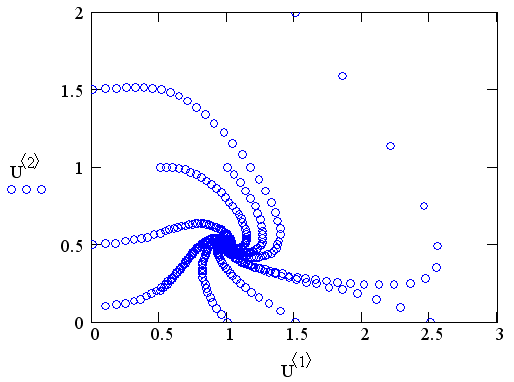
Рис. 11.14. Фазовый портрет брюсселятора при в=0.5 (листинг 11.10)
Как видно из рис. 11.14, все траектории, вышедшие из разных точек, асимптотически стремятся к одному и тому же аттрактору (1.0.5). Из теории динамических систем нам известно, что такой аттрактор называется узлом (с узлом мы уже встречались в примерах разд. 11.1). Конечно, в общем случае при анализе фазового портрета желательно "прощупать" большее число траекторий, задавая более широкий диапазон начальных условий. Не исключено, что в других областях фазовой плоскости траектории будут сходиться к другим аттракторам.
Эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром в. При его увеличении узел будет сначала постепенно смещаться в точку с координатами (1,в), пока не достигнет бифуркационного значения в=2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. При дальнейшем увеличении в происходит лишь количественное изменение параметров этого цикла. Решение, полученное при в=2.5, показано на рис. 11.15.
Чтобы найти аттракторы динамической системы, как известно, нужно решить систему алгебраических уравнений, получающуюся из системы ОДУ заменой нулями их левых частей. Эти задачи также удобно решать средствами Mathcad (см. гл. 8). В частности, исследование зависимости фазового портрета от параметров системы ОДУ и поиск бифуркаций можно проводить методами продолжения (см. разд. "Метод продолжения по параметру" гл. 8).
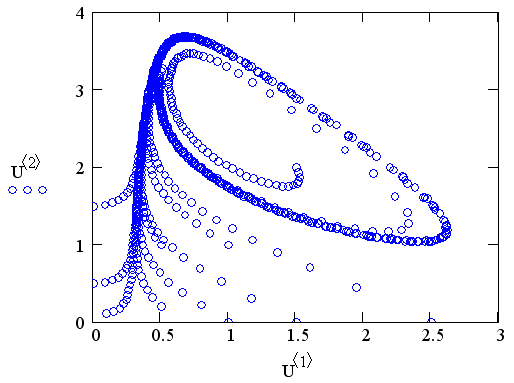
Рис. 11.15. Фазовый портрет брюсселятора при в=2.5
Читатели, сталкивающиеся с расчетом динамических систем, несомненно оценят возможности Mathcad по построению фазовых портретов и исследованию бифуркаций. Возможно также, что они найдут лучшие программные решения этой задачи, чем алгоритм, предложенный в данном разделе автором.
