Встроенные функции rkfixed, Rkadapt, Bulstoer
Альтернативный метод решения ОДУ перешел из прежних версий Mathcad. Он заключается в использовании одной из встроенных функций rkfixed, Rkadapt или Bulstoer. Этот способ несколько проигрывает первому и в простоте, и в наглядности. Поэтому я советую предпочесть вычислительный блок Given/odesoive. Однако иногда приходится решать ОДУ первого порядка с помощью второго способа, например, при следующих обстоятельствах:
- одно ОДУ решается в контексте решения более сложных задач, в которые входят системы дифференциальных уравнений (для которых вычислительный блок неприменим) – в этом случае может потребоваться единый стиль программирования;
- ответ предпочтительнее получить в виде вектора, а не функции;
- Вы привыкли к записи ОДУ в старых версиях Mathcad, у Вас много документов, созданных с их помощью и т.п.
Поскольку решение вторым способом одного ОДУ мало чем отличается от решения систем ОДУ (см разд 11.3), приведем пример его использования в задаче из листинга 11.1. практически без комментариев (см. листинг 11.2) и с помощью одной из трех существующих для этих целей встроенных функций rkfixed. Обратите внимание только на необходимость явного задания количества точек интегрирования ОДУ м=100 в третьей строке листинга, а также на получение результата, в отличие от вычислительного блока, не в виде функции, а в виде матрицы размерности M X 2. Она состоит из двух столбцов в одном находятся значения аргумента t (от t0 до t1 включительно), а в другом соответствующие значения искомой функции y(t).
Листинг 11.2. Решение задачи Коши для ОДУ первого порядка вторым способом:
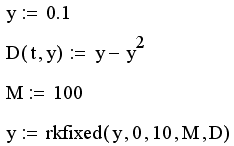
В листинге 11.2. приведен пример не лучшего стиля Mathcad-программирования. Сначала переменной у присвоено значение скаляра у=0 1, а затем этой же переменной присвоено матричное значение (результат решения ОДУ). Старайтесь избегать такого стиля, который ухудшает читаемость программы и может приводить, в более сложных случаях, к трудно опознаваемым ошибкам. Неплохим решением было бы назвать результат по-другому, например u.
График решения рассматриваемого уравнения показан на рис. 11.1. Обратите внимание, что он соответствует получению решения в матричном виде (листинг 11.2), поэтому по осям отложены соответствующие столбцы, выделенные из матрицы у оператором <>.
Пример, решенный в листингах 11.1-11.2, взят из области математической экологии и описывает динамику популяций с внутривидовой конкуренцией. Сначала происходит рост численности популяции, близкий к экспоненциальному, а затем выход на стационарное состояние.
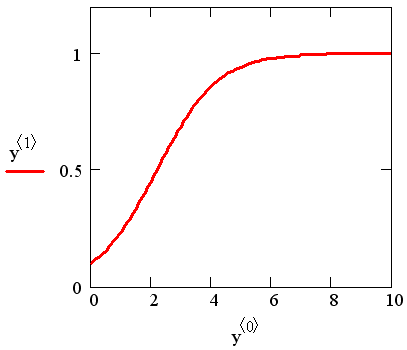
Рис. 11.1. Решение уравнения y' =y-y2 (листинг 11.2)
