Градиентные методы: функция Find
Если вы решаете "хорошие" уравнения, как все те, которые были приведены в предыдущих разделах, то, вообще говоря, можете никогда не задумываться, как именно Find ищет их корни. Однако даже в этом случае полезно представлять, что происходит "за кадром", т. е. какие действия совершаются в промежутке между введением необходимых условий после ключевого слова Given и получением результата после применения функции Find. Это важно хотя бы с позиций выбора начальных значений переменных перед вычислительным блоком. Рассмотрим в данном разделе некоторые особенности численных методов и возможности установки их различных параметров, которые предоставляет Find.
Принцип действия градиентных алгоритмов
Во встроенной функции Find реализовано несколько градиентных численных алгоритмов, один из которых может выбрать либо программа Mathcad, либо сам пользователь. Покажем их основную идею на примере уравнения с одним неизвестным f (x)=0 для функции f(х)=х2 +5х+2, график которой показан на рис. 5.8. Принцип градиентных методов состоит в последовательных приближениях к истинному решению уравнения, которые вычисляются с помощью производной от f (х). Приведем наиболее простую форму алгоритма, называемого методом Ньютона:
- За нулевую итерацию принимается введенное пользователем начальное значение х0=х.
- В точке х0 методом конечных разностей вычисляется производная f (x0).
- Пользуясь разложением Тейлора, можно заменить f (х) в окрестности х0 касательной – прямой линией f (x)=f (x0) +f (х0)-(х-х0).
- Определяется точка x1, в которой прямая пересекает ось х (рис. 5.8).
- Если f (x1)<TOL, то итерации прерываются, и значение x1 выдается в качестве решения. В противном случае x1 принимается за новую итерацию, и цикл повторяется: строится касательная к f (х) в точке x1, определяется х2 – точка ее пересечения с осью х и т.д.
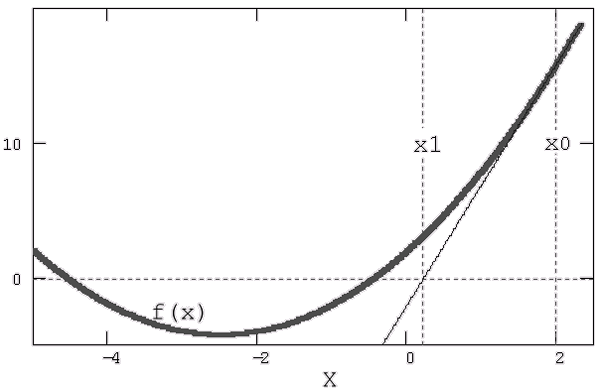
Рис. 5.8. Иллюстрация метода Ньютона
Модификация алгоритма Ньютона для решения системы нескольких уравнений заключается в линеаризации соответствующих функций многих переменных, т. е. аппроксимации их линейной зависимостью с помощью частных производных.
Например, для нулевой итерации в случае системы двух уравнений используются выражения типа:
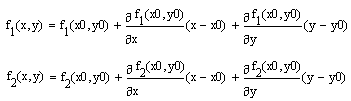
Чтобы отыскать точку, соответствующую каждой новой итерации, требуется приравнять оба равенства нулю, т. е. решить на каждом шаге полученную систему линейных уравнений.
