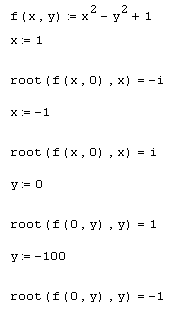Уравнение с одним неизвестным: функция root
Листинг 5.14. Пример уравнения, которое удается решить только методом секущих:

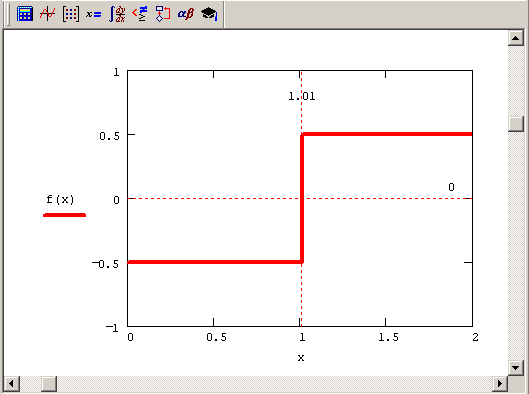
Рис. 5.5. Модельная функция f (х) (продолжение листинга 5.14)
Остается добавить, что f (х) может быть функцией не только х, а любого количества аргументов. Именно поэтому в самой функции root необходимо определить, относительно какого из аргументов следует решить уравнение. Эта возможность проиллюстрирована листингом 5.15 на примере функции двух переменных f (x,y)=x2 -y2 +1. В нем сначала решается уравнение f (х, 0) =0 относительно переменной х, а потом – другое уравнение f (0, у) =0 относительно переменной у, причем, благодаря удачному подбору начальных значений, вычисляются все корни данного квадратичного уравнения.
Таким образом, в обоих случаях один из аргументов функции f (х) воспринимается как неизвестное, а другой – как параметр. Не забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки "This variable or function is not defined above", в данном случае говорящей о том, что другая переменная ранее не определена.
Примечание
Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 5.3.3.
Листинг 5.15. Поиск корней уравнения, зависящего от двух переменных: