Иллюстрированный самоучитель по MathCAD 12

Численное решение уравнений. Системы уравнений: функция Find.

Как правило, отыскание корней алгебраического уравнения (или системы уравнений) численными методами связано с двумя задачами:

• локализация корней, т. е. определение их существования в принципе, а также исследование их количества и примерного расположения;
• собственно отыскание корней с заданной погрешностью (в Mathcad ее роль играет системная константа TOL).

Последнее означает, что надо найти значения х₀, при которых f(х₀) отличается от нуля не более чем на TOL. Почти все встроенные функции системы Mathcad, предназначенные для решения нелинейных алгебраических уравнений (в том числе функция Find применительно к численному процессору) нацелены на решение второй задачи, т. е. предполагают, что корни уже приблизительно локализованы. Иными словами, перед тем, как непосредственно приступать к нахождению корней уравнения, необходимо (хотя бы приблизительно) представлять себе, где они находятся. Имея в виду данную оговорку, мы перейдем к рассмотрению второй из задач, а проблему предварительной локализации корней рассмотрим в конце данного раздела.

Системы уравнений: функция Find

Рассмотрим решение системы N нелинейных уравнений с м неизвестными:

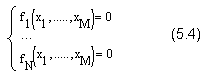
Здесь f₁(x₁,…, х_M),…, f_N (x₁,…, X_M) – некоторые скалярные функции от скалярных переменных x₁,x₂,…, х_M и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (5.4) можно формально переписать в виде:

Где х – вектор, составленный из переменных x₁,x₂,…,х_M, а f (х) – соответствующая векторная функция.

Вычислительный блок Given/Find

Для численного решения систем уравнений применяется тот же самый вычислительный блок, что и для символьных вычислений (см. разд. 5.1.1). Повторимся, что он состоит из ключевого слова Given, самой системы уравнений, записанной при помощи логических операторов панели Boolean (Булевы операторы), а также встроенной функции Find. Find(x₁,…,х_M) – встроенная функция для решения системы алгебраических уравнений и неравенств относительно переменных x₁,…,x_M. Значение функции Find представляет собой вектор, составленный из решений по каждой переменной.

Примечание 1
Встроенная функция Find использует в качестве численного алгоритма один из градиентных методов (см. разд. 5.3). Этот факт налагает некоторые ограничения на уравнения системы, которые должны быть достаточно гладкими функциями своих аргументов.

Примечание 2
При численных расчетах может быть найден только один из корней уравнения, в отличие от символьных вычислений, которые позволяют определить все имеющиеся корни.

Применение численного нахождения корней отличается от символьного двумя обстоятельствами:

• вместо оператора символьного вывода после функции Find следует использовать оператор численного вывода (знак равенства);
• перед вычислительным блоком Given/Find должны быть заданы начальные значения (guess value) для всех неизвестных, т. е. всем переменным x₁,…,х_M, относительно которых решается уравнение, следует предварительно присвоить некоторые численные значения, с которых и будет начинаться поиск корня. Таким образом, присвоение начального значения требует априорной информации о примерном местонахождении корня и связано с проблемой локализации корней, упомянутой в начале разд. 5.2.

Примечание
Помните также о том, что, в отличие от символьного, для численного процессора необходимо задать числовые значения всех параметров, входящих в уравнение.