Иллюстрированный самоучитель по MathCAD 12

Корни полинома: функция polyroots

Если функция f (х) является полиномом, то все его корни можно определить, используя встроенную функцию:

• polyroots(v):
  • где v – вектор, составленный из коэффициентов полинома.

Поскольку полином N -й степени имеет ровно N корней (некоторые из них могут быть кратными), вектор v должен состоять из N+1 элемента. В основе встроенной функции polyroots лежат специфические численные алгоритмы, а результатом ее действия является вектор, составленный из N корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root. Пример поиска корней полинома четвертой степени иллюстрируется листингом 5.16.

Коэффициенты рассматриваемого в примере полинома записаны в виде вектора в первой строке листинга:

f (х) = (х-3)-(х-1)³ =х⁴ -6х³ +12х² -10х+3

Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х1 и т. д. Соответственно, последним N+1 элементом вектора должен быть коэффициент при старшей степени x^N.

Совет
Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пункт Expand (Разложить). В результате символьный процессор Mathcad сам преобразует полином в нужную форму; пользователю надо будет только корректно ввести ее в аргументы функции polyroots.

Листинг 5.16. Вычисление корней полинома:

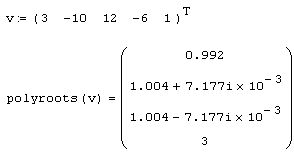
Обратим внимание на результат применения функции polyroots, заметив, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.

Для функции polyroots можно выбрать один из двух численных методов – метод полиномов Лаггера (он установлен по умолчанию) или метод парной матрицы.

Для смены метода:

1. Вызовите контекстное меню, щелкнув правой кнопкой мыши на слове polyroots.
2. В верхней части контекстного меню выберите либо пункт LaGuerre (Лаггера), либо Companion Matrix (Парная матрица).
3. Щелкните правой кнопкой мыши вне действия функции polyroots – если включен режим автоматических вычислений, будет произведен пересчет корней полинома в соответствии с вновь выбранным методом.

Для того чтобы оставить за Mathcad выбор метода решения, установите флажок AutoSelect (Автоматический выбор), выбрав одноименный пункт в том же самом контекстном меню.