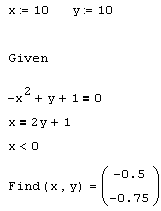Численное решение уравнений. Системы уравнений: функция Find.
Системы уравнений
Приведем еще один пример численного решения алгебраических уравнений, обратившись на этот раз к системе двух уравнений, которая также уже исследовалась нами при помощи символьного процессора. Система имеет два решения, показанные графически на рис. 5.2 и найденные аналитически в листинге 5.7 (см. разд 5.1.3). Листинг 5.10, демонстрирующий численное решение рассматриваемой системы, начинается с присвоения неизвестным начальных значений х=10, у=10. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. В результате (последняя строка листинга) Mathcad находит один из корней х=1, у=0, причем первый элемент вектора решения есть первый аргумент функции Find, а второй элемент – ее второй аргумент. Поскольку решение производится численным методом, оно выдается с некоторой погрешностью, не превышающей встроенной константы CTOL. Если задать в первой строке листинга другие начальные значения, расположенные ближе к другому корню, например, х=0,у=0, то найден в итоге будет другой корень х=-0.5, у=-0.75.
Примечание 1
На самом деле в вычислительном блоке используются обе системные константы Mathcad, связанные с заданием погрешности: TOL и CTOL. Константа CTOL ограничивает невязку, т. е. задает точность выполнения уравнений, введенных после ключевого слова Given. Например, если CTOL=0.001, то уравнение х=10 будет считаться выполненным и при х=10.001, и при х=9.999. Другая константа TOL определяет условие прекращения итераций численным алгоритмом (см. разд. 5.4). Значение CTOL может быть задано пользователем так же, как и TOL, например, CTOL=0.01. По умолчанию принято, что CTOL= =TOL=0.001, но вы по желанию можете переопределить их.
Примечание 2
Часто бывает очень полезным проверить точность решения уравнений "вручную", подставив найденные вычислительным процессором корни в исходные уравнения и оценив значение их невязок.
Листинг 5.10. Численное решение системы алгебраических уравнений:
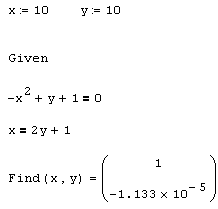
Если предпринять попытку решить несовместную систему, в частности, в рассматриваемом примере добавить еще одно уравнение, то Mathcad выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.
Особую осторожность следует соблюдать при решении систем с числом неизвестных большим, чем число уравнений. Например, можно удалить одно из двух уравнений из рассмотренной нами задачи, попытавшись решить оставшееся единственное уравнение с двумя неизвестными х и у (листинг 5.11). В такой постановке задача имеет бесконечное множество корней: для любого х и, соответственно, у=х2 -1 условие, определяющее единственное уравнение, выполнено. Однако даже если корней бесконечно много, численный метод будет производить расчеты только до тех пор, пока логические выражения в вычислительном блоке не будут выполнены (конечно, в пределах погрешности). После этого итерации будут остановлены и выдано решение. В результате будет найдена всего одна пара значений (х,у), обнаруженная первой, как это показано в последней строке листинга 5.11.
Примечание
Для того чтобы найти все решения рассматриваемой задачи, можно обратиться к возможностям символьного процессора Mathcad. Достаточно в последней строке листинга заменить знак равенства на оператор символьного вывода, и в качестве ответа будет выдано семейство решений х и х2 -1.
Листинг 5.11. Численное решение уравнения, имеющего бесконечное множество корней, приводит к одному из них:
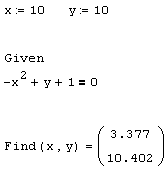
Системы уравнений и неравенств
Пока мы рассматривали примеры систем уравнений, число которых было таким же, как и число неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х в рассмотренный выше листинг 5.10 приведет к нахождению другого решения, как это показано в листинге 5.12.
Обратите внимание, что, несмотря на те же начальные значения, что и в листинге 5.10, в листинге 5.12 мы получили другой корень системы уравнений. Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке листинга 5.12.
Листинг 5.12. Численное решение системы алгебраических уравнений и неравенств:
