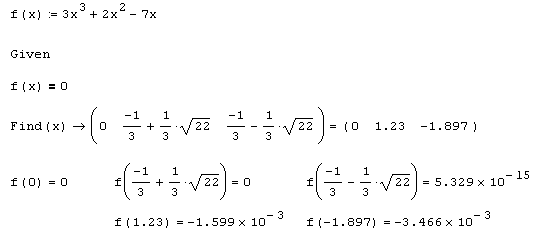Одно уравнение
Поясним сказанное на примере решения одного (кубического) уравнения с одним неизвестным х (рис. 5.1):
3 * x ^ 3 + 2 * x ^ 2 - 7 * x = 0, (5.3)Листинг 5.1. Аналитическое решение кубического уравнения:
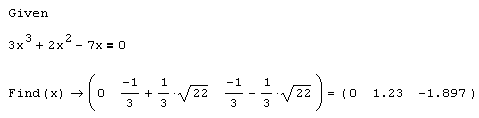
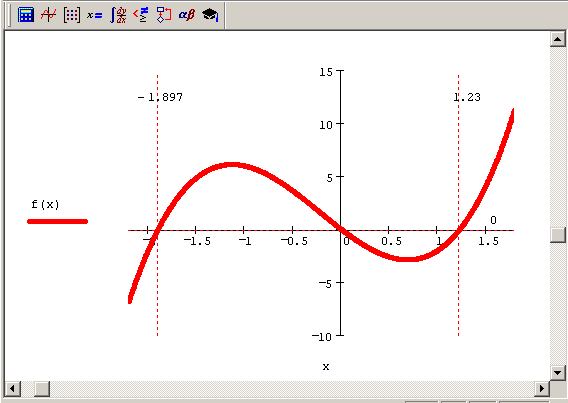
Рис. 5.1. График функции f (х) =3х3+2х2-7х
В листинге 5.1 вы видите все три последовательные строки вычислительного блока. Первая строка представляет собой обязательное ключевое слово Given, следующая строка является, собственно, записью уравнения (5.3), а в последней строке листинга включается в работу встроенная функция Find. Обратите внимание, что после имени функции Find находится оператор символьного вывода, справа от которого (по истечении необходимого времени работы символьного процессора) возникает аналитический результат решения уравнения. Существенно, что он является точным решением (записанным в данном случае в трансцендентном виде), а получить числовые значения корней можно, поставив после него символ численного равенства (как это сделано в последней строке листинга 5.1).
Как видно из листинга 5.1, уравнение имеет три различных корня, которые представляются справа от функции соответствующим трехкомпонентным вектором. Таким образом, решение предлагается пользователю в форме матрицы размера 1хз (одна неизвестная переменная имеет три значения, каждое из которых обращает уравнение в тождество).
Пример, использованный в листинге 5.1, включает уравнение, записанное в традиционной форме равенства. Приведем решение того же самого уравнения, если оно представлено в несколько другой форме, подчеркивающей специфику задачи нахождения корней функции (листинг 5.2). Основное отличие листинга 5.2 от предыдущего связано с другой формой записи исследуемого уравнения через функцию пользователя f (x). Иными словами, подчеркивается специфика поставленной задачи отыскания нулевых значений некоторой функции.
Важно заметить, что точное решение уравнения (непосредственно после оператора символьного вывода результата работы функции Find) обращает f (х) в тождественный ноль, а пересчитанные числовые значения корней (после знака обычного равенства) обеспечивают лишь ее приближенное равенство нулю (разумеется, это связано с ошибками округления).
Внимание!
Не забывайте о том, что вводить знаки равенства в уравнение в пределах вычислительного блока Given/Find следует при помощи панели Boolean (Булевы операторы).
Листинг 5.2. Аналитический поиск нулей функции f(x):
