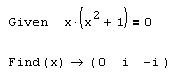Одно уравнение
В заключение разговора о символьном решении уравнений с одним неизвестным приведем еще два показательных примера, связанных с нахождением нулей функции нескольких аргументов (т. е. зависящих, помимо, собственно, неизвестного, еще и от дополнительных параметров). Листинг 5.3 демонстрирует, как выглядит решение уравнения, включающего четыре различные переменные, по некоторым из этих переменных. Обратите внимание на последний из трех приведенных в листинге 5.3 примеров, иллюстрирующий результат решения уравнения относительно сразу всех входящих в него параметров.
Помните, что для корректной работы символьного процессора вовсе не обязательно задавать конкретные значения переменных, входящих в уравнение, а если такие значения (для некоторых, либо всех, параметров) определены, то это учитывается при выводе результата (что иллюстрируется листингом 5.4).
Листинг 5.3. Символьное решение уравнения относительно разных переменных:
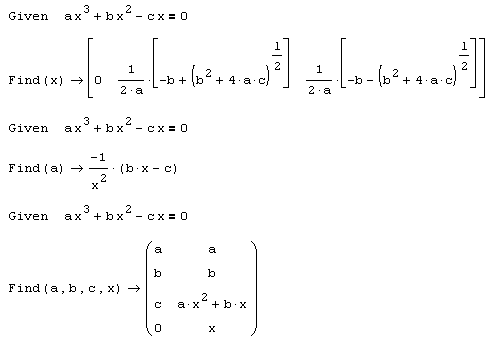
Листинг 5.4. Символьное решение уравнения, зависящего от параметров, в случае предварительного задания их числовых значений:
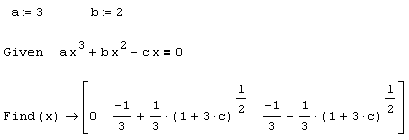
Если решить уравнение аналитически не удается, то результатом применения оператора символьного вывода после функции Find будет либо тривиальное выражение типа Find(x) › x (как в листинге 5.5), либо сообщение об ошибке "No symbolic result was found" (Ни один символьный результат не найден). Следует помнить, что символьный процессор Mathcad "умеет" находить не только действительные, но и комплексные корни уравнений. В качестве примера приведем листинг 5.6 с решением кубического уравнения, имеющего три очевидных корня – одного действительного (равного нулю) и двух чисто мнимых (±i, где i – мнимая единица).
Листинг 5.5. Решить уравнение аналитически не удается:
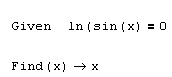
Листинг 5.6. Символьное решение уравнения, имеющего и действительные, и мнимые корни: