Сглаживание и фильтрация. Встроенные функции для сглаживания: ВЧ-фильтр.
При анализе данных часто возникает задача их фильтрации, заключающаяся в устранении одной из составляющих зависимости y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые чаще всего обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая. В связи с этим считают, что сглаживание является частным случаем более общей задачи фильтрации сигнала, которая связана с подавлением определенных диапазонов частот спектра.
Наиболее простым и эффективным рецептом сглаживания (smoothing) можно считать регрессию различного вида, разобранную в предыдущей главе (см. разд. 13.2). Однако регрессия часто уничтожает информативную составляющую данных, оставляя лишь наперед заданную пользователем зависимость.
Часто рассматривают противоположную задачу фильтрации – устранение медленно меняющихся вариаций в целях исследования высокочастотной составляющей. В этом случае говорят о задаче устранения тренда. Иногда интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением полосовой фильтрации.
Несколько примеров программной реализации различных вариантов фильтрации приведены в данном разделе.
Встроенные функции для сглаживания: ВЧ-фильтр
В Mathcad имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных:
- medsmooth(y,b) – сглаживание алгоритмом "бегущих медиан";
- ksmooth(х,у,b) – сглаживание на основе функции Гаусса;
- supsmooth(x,y) – локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных:
- х – вектор действительных данных аргумента (для supsmooth его элементы должны быть расположены в порядке возрастания);
- у – вектор действительных значений того же размера, что и х;
- b – ширина окна сглаживания.
Все функции имеют в качестве аргумента векторы, составленные из массива данных, и выдают в качестве результата вектор сглаженных данных того же размера. Функция medsmooth предполагает, что данные расположены равномерно.
Примечание
Подробную информацию об алгоритмах, заложенных в функции сглаживания, вы найдете в справочной системе Mathcad в статье Smoothing (Сглаживание), находящейся в разделе Statistics (Статистика). Очень полезные сведения о разных типах фильтрации можно отыскать в Быстрых шпаргалках.
Часто бывает полезным совместить сглаживание с последующей интерполяцией или регрессией. Соответствующий пример приведен в листинге 14.7 для функции supsmooth. Результат работы листинга показан на рис. 14.18 (кружки обозначают исходные данные, крестики – сглаженные, пунктирная кривая – результат сплайн-интерполяции). Сглаживание тех же данных при помощи "бегущих медиан" и функции Гаусса с разным значением ширины окна пропускания показаны на рис. 14.19 и 14.20 соответственно.
Листинг 14.7. Сглаживание с последующей сплайн-интерполяцией:

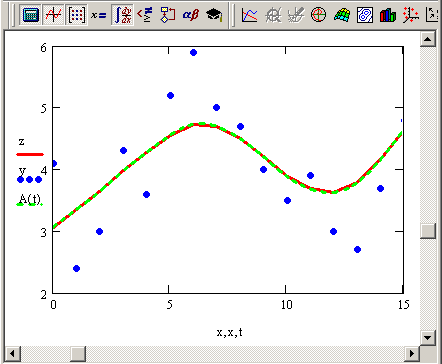
Рис. 14.18. Адаптивное сглаживание (продолжение листинга 14.7)
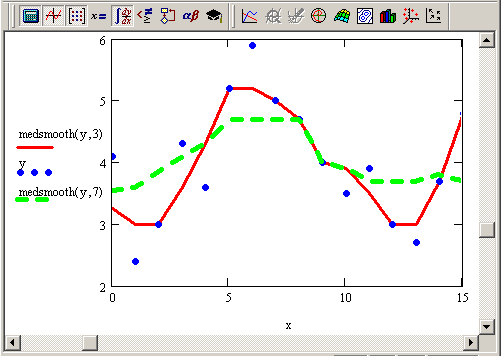
Рис. 14.19. Сглаживание "бегущими медианами"
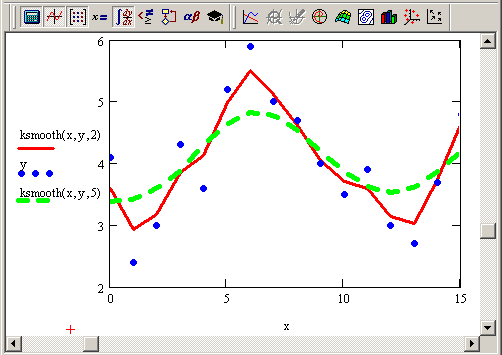
Рис. 14.20. Сглаживание при помощи функции ksmooth
