Обратное преобразование Фурье
Для расчета обратного Фурье-преобразования (восстановления сигнала по имеющемуся действительному спектру) следует использовать следующие встроенные функции (они также реализуют алгоритм БПФ):
- ifft (v) – вектор обратного действительного преобразования Фурье;
- IFFT(V) – вектор обратного действительного преобразования Фурье в другой нормировке:
- v – вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.
Примечание
Аргумент (вектор v) функций, реализующих обратное преобразование Фурье, может быть как действительным, так и комплексным. А вот результат их работы является вектором, составленным из действительных чисел. Если аргумент является N-компонентным вектором, где N=l+2n, то в результате получается в два раза больший вектор из 2 (N-1) =2n+1 компонент.
Результат обратного преобразования Фурье спектра, представленного на рис. 14.2 и 14.3, показан в виде кружков на рис. 14.5 вместе с исходными данными.
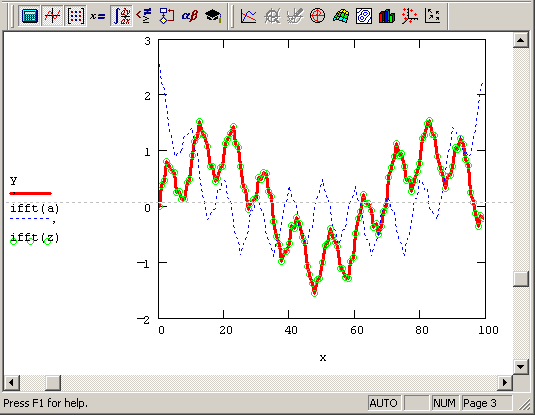
Рис. 14.5. Обратное преобразование Фурье (продолжение листинга 14.1)
Видно, что в рассматриваемом случае сигнал у(х) восстановлен с большой точностью, что характерно для плавного изменения сигнала. Если же в качестве аргумента функции ifft использовать модуль Фурье-спектра (мы присвоили этому вектору в листинге 14.1 имя а), то профиль исходного сигнала будет реконструирован правильно, но окажется сдвинутым на определенное расстояние вдоль оси х. Так происходит из-за того, что взятие абсолютной величины комплексного спектра уничтожает информацию об относительной фазе отсчетов данных.
