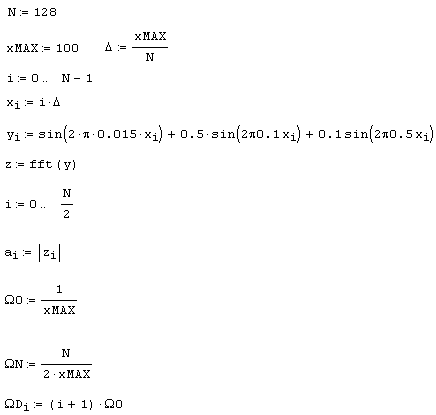Фурье-спектр. Фурье-спектр действительных данных.
Интегральные преобразования массива сигнала у(х) ставят в соответствие всей совокупности данных у(х) некоторую функцию другой координаты F(v). Рассмотрим встроенные функции для расчета интегральных преобразований, реализованных в Mathcad.
Математический смысл преобразования Фурье состоит в представлении сигнала у(х) в виде бесконечной суммы синусоид вида F(v)sin(v-x). Функция F(V) называется преобразованием Фурье, или интегралом Фурье, или Фурье-спектром сигнала. Ее аргумент v имеет смысл частоты соответствующей составляющей сигнала. Обратное преобразование Фурье переводит спектр F(V) в исходный сигнал у (х). Согласно определению:
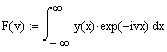
Как видно, преобразование Фурье является комплексной величиной, даже если сигнал действительный.
Фурье-спектр действительных данных
Преобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм, называемый БПФ (быстрое преобразование Фурье). Рассмотрим сначала наиболее типичную для физического эксперимента ситуацию расчета Фурье-спектра действительного сигнала, для которой алгоритм БПФ реализован в нескольких встроенных функциях Mathcad, различающихся нормировками:
- fft (у) – вектор прямого преобразования Фурье;
- FFT (у) – вектор прямого преобразования Фурье в другой нормировке:
- у – вектор действительных данных, взятых через равные промежутки значений аргумента.
Внимание!
Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно 2n элементов (n – целое число). Результатом является вектор с 1+2n-1 элементами. Если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями, иначе вместо решения появится сообщение об ошибке.
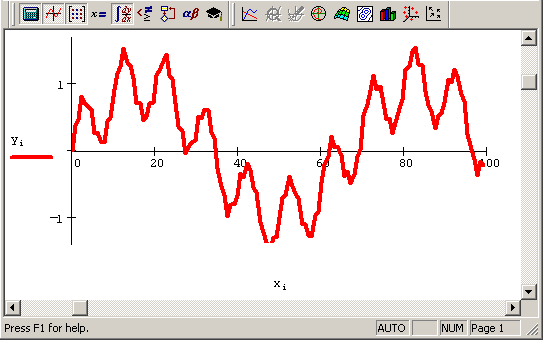
Рис. 14.1. Исходные модельные данные (продолжение листинга 14.1)
Чтобы смысл преобразования Фурье был более понятен, используем в качестве модельных данных дискретизацию детерминированного сигнала,, равного сумме трех синусоид (рис. 14.1). Листинг 14.1 демонстрирует расчет Фурье-спектра по N=128 точкам, причем предполагается, что интервал дискретизации данных yi равен Δ. В середине листинга применяется встроенная функция fft, а его оставшаяся часть предназначена для корректного пересчета соответствующих значений частот Ωi (они вычисляются в последней строке листинга). Обратите внимание, что результаты расчета представляются в виде модуля Фурье-спектра (рис. 14.2), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра (рис. 14.3) с определением синусоид в листинге 14.1.
Листинг 14.1. Быстрое преобразование Фурье:
