Встроенная функция вейвлет-преобразования
Mathcad имеет одну встроенную функцию для расчета вейвлет-преобразования на основе вейвлетобразующей функции Добеши:
- wave (у) – вектор прямого вейвлет-преобразования;
- iwave (v) – вектор обратного вейвлет-преобразования:
- у – вектор данных, взятых через равные промежутки значений аргумента;
- v – вектор данных вейвлет-спектра.
Аргумент функции вейвлет-преобразования, т. е. вектор у, должен так же, как и в преобразовании Фурье, иметь ровно 2n элементов (n – целое число). Результатом функции wave является вектор, скомпонованный из нескольких коэффициентов с двухпараметрического вейвлет-спектра.
Использование функции wave объясняется на примере анализа суммы двух синусоид в листинге 14.5, а три семейства коэффициентов вычисленного вейвлет-спектра показаны на рис. 14.16.
Листинг 14.5. Поиск вейвлет-спектра Добеши:

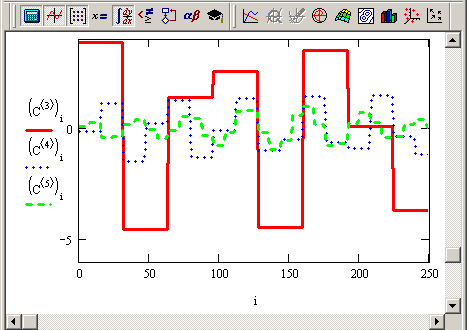
Рис. 14.16. Вейвлет-спектр на основе функции Добеши (продолжение листинга 14.5)
