Фурье-спектр. Фурье-спектр действительных данных.
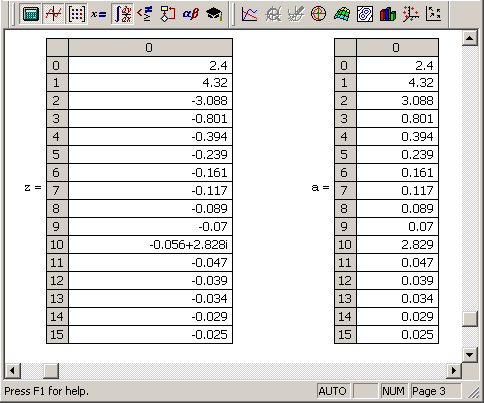
Рис. 14.2. Матрица-результат вычисления Фурье-спектра данных (продолжение листинга 14.1)
Исключительно важными представляются два параметра, заданные в предпоследней строке листинга 14.1, называемые соответственно граничной частотой и частотой Найквиста. Граничная частота Ω 0 определяет нижнюю, а частота Найквиста Ω N – верхнюю границу аргумента вычисленного спектра, как показано маркерами на рис. 14.3. Кроме того, важно, что интервал дискретизации Фурье-спектра также равен Ω0, а общее число вычисляемых точек спектра составляет N/2 (в нашем примере N/2=64). Последние утверждения иллюстрируются маркерами на рис. 14.4, изображающем график Фурье-спектра вблизи нижней границы частот.
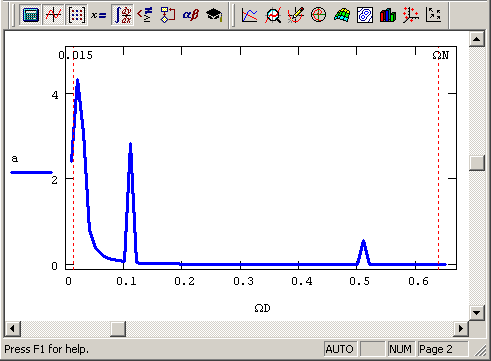
Рис. 14.3. График Фурье-спектра данных (продолжение листинга 14.1)
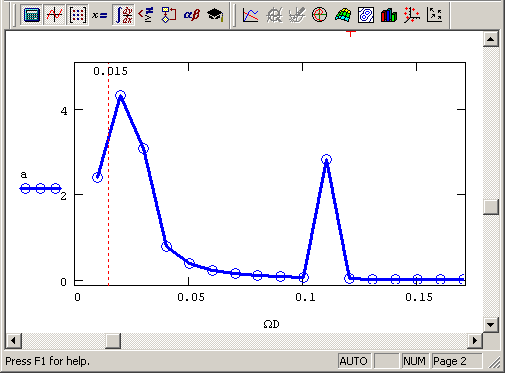
Рис. 14.4. Низкочастотная область Фурье-спектра (продолжение листинга 14.1)
