Иллюстрированный самоучитель по MatLab

Элементарные средства решения СЛУ

В этом большом уроке описываются функции системы MATLAB, предназначенные для реализации алгоритмов типовых численных методов решения прикладных задач и обработки данных. Наряду с базовыми операциями решения систем линейных и нелинейных уравнений рассмотрены функции вычисления конечных разностей, численного дифференцирования, численного интегрирования, триангуляции, аппроксимации Лапласиана и, наконец, прямого и обратного преобразования Фурье. Отдельные разделы посвящены работе с полиномами и численным методам решения обыкновенных дифференциальных уравнений. Этот большой урок стоит разбить на две-три части или изучать выборочно.

Решение систем линейных уравнений (СЛУ) относится к самой массовой области применения матричных методов, описанных в уроках 10-12. В этом разделе вы найдете ответы на вопросы, каким образом применяются указанные методы и какие дополнительные функции имеет система MATLAB для решения систем линейных уравнений.

Как известно, обычная СЛУ имеет вид:

а ₁₁ X ₁ , а ₁₂ , X ₂ …, а _1n X _n = b ₁

Здесь а ₁₁ , а, ₂ ,…, а _nn– коэффициенты, образующие матрицу А, которые могут иметь действительные или комплексные значения, x ₁ , х ₂ ,…, х _п– неизвестные, образующие вектор X, и b ₁ , b ₂ ,…, b _n – свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А – матрица коэффициентов уравнений, X – искомый вектор неизвестных и В – вектор свободных членов. В зависимости от вида матрицы А и ее характерных особенностей MATLAB позволяет реализовать различные методы решения.

Для реализации различных алгоритмов решения СЛУ и связанных с ними матричных операций применяются следующие операторы: +,-,*,/, \, *, '. Как отмечалось ранее, MATLAB имеет два различных типа арифметических операций – поэлементные и для массивов (векторов и матриц) в целом. Матричные арифметические операции определяются правилами линейной алгебры.

Арифметические операции сложения и вычитания над массивами выполняются поэлементно. Знак точки "." отличает операции над элементами массивов от матричных операций. Однако, поскольку операции сложения и вычитания одинаковы для матрицы и элементов массива, знаки ".+" и ".-" не используются. Рассмотрим другие операторы и выполняемые ими операции.

• * – матричное умножение;
• С = А*В – линейное алгебраическое произведение матриц А и В:

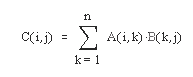
Для случая нескалярных А и В число столбцов матрицы А должно равняться числу строк матрицы В. Скаляр может умножаться на матрицу любого размера.

• / – правое деление. Выражение Х=В/А дает решение ряда систем линейных уравнений АХ=В, где А – матрица размера тхп и В – матрица размера nxk;
• \ – левое деление. Выражение Х=В\А дает решение ряда систем линейных уравнений ХА=В, где А – матрица размера тхп и В – матрица размера nxk. Если А – квадратная матрица, то А\В – примерно то же самое, что и inv(A)*B, в остальных случаях возможны варианты, отмеченные ниже.

Если А – матрица размера пхп, а В – вектор-столбец с п компонентами или матрица с несколькими подобными столбцами, тогда Х=А\В – решение уравнения АХ=В, которое находится хорошо известным методом исключения Гаусса.

Если А – матрица размера тхп и тхп, а В представляет собой вектор-столбец с m компонентами или матрицу с несколькими такими столбцами, тогда система оказывается недоопределенной или переопределенной и решается на основе минимизации второй нормы невязок.

Ранг k матрицы А находится на основе QR-разложения (урок 11) с выбором ведущего элемента. Полученное решение X будет иметь не больше чем k ненулевых компонентов на столбец. Если k<n, то решение, как правило, не будет совпадать с pinv(A)*B, которое имеет наименьшую норму невязок ||Х||.

• ^ – возведение матрицы в степень. Х^А р – это X в степени р, если р – скаляр. Если р – целое число, то степень матрицы вычисляется путем умножения X на себя р раз. Если р – целое отрицательное число, то X сначала инвертируется. Для других значений р вычисляются собственные значения и собственные векторы, так что если [V.D]=eig(X), то X*p=V*D.^A p/V. Если X – скаляр и Р – матрица, то Х^А Р – это скаляр X, возведенный в матричную степень Р. Если X и Р – матрицы, то Х^Л Р становится некорректной операцией и система выдает сообщение об ошибке. Возможный вариант решения матричного уравнения АХ=В с применением оператора^{^} можно представить как Х=В*А^{^} -1.
• ' – транспонирование матрицы, то есть замена строк столбцами и наоборот. Например, А' – транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Транспонирование при решении СЛУ полезно, если в матрице А переставлены местами столбцы и строки.

При записи СЛУ в матричной форме необходимо следить за правильностью записи матрицы А и вектора В. Пример (в виде m-файла):

Эта программа выдает результаты решения тремя способами:

Как и следовало ожидать, результаты оказываются одинаковыми для всех трех методов. При решении систем линейных уравнений, особенно с разреженной матрицей коэффициентов, полезно применение функций colmmd (colamd), symmmd (symamd), описанных ранее в уроке 12.