Вычисление полиномов. Вычисление производной полинома.
В этом разделе приведены функции вычисления коэффициентов характеристического полинома, значения полинома в точке и матричного полинома.
- poly(A) – для квадратной матрицы А размера пхп возвращает вектор-строку размером n+1, элементы которой являются коэффициентами характеристического полинома det(A-sI), где I – единичная матрица, as – оператор Лапласа. Коэффициенты упорядочены по убыванию степеней. Если вектор состоит из п+1 компонентов, то ему соответствует полином вида c 1 s^n+…+c n s+c n+1 ;
- poly (г) – для вектора г возвращает вектор-строку р с элементами, представляющими собой коэффициенты полинома, корнями которого являются элементы вектора г. Функция roots(p) является обратной, ее результаты, умноженные на целое число, дают poly (r).
A =2 3 63 8 61 7 4>> d=poly(A) d =1.0000-14.0000-1.0000-40.0000>> A=[3.6.8:12.23.5:11.12.32] A =3 6 81223 51112 32>> poly(A) ans =1.0000-58.0000 681.0000 818.0000Приведенная ниже функция вычисляет корни (в том числе комплексные) для полинома вида:
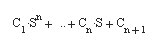
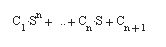
- roots (с) – возвращает вектор-столбец, чьи элементы являются корнями полинома с.
Вектор-строка с содержит коэффициенты полинома, упорядоченные по убыванию степеней. Если с имеет n+1 компонентов, то полином, представленный этим вектором, имеет вид. Пример:
>> x=[7.45.12.23];d=roots(x) d =-6.2382-0.0952+0.7195i-0.0952-0.7195iA=[-6.2382-0.0952+0.71951-0.0952-0.71951]: B=Poly (A) B=[1.0000 6.4286 1.7145 3.2859] B*7ans =7.0000 45.000212.001523.0013С погрешностью округления получили тот же вектор.
- polyval (p,x) – возвращает значения полинома р, вычисленные в точках, заданных в массиве х. Полином р – вектор, элементы которого являются коэффициентами полинома в порядке уменьшения степеней, х может быть матрицей или вектором. В любом случае функция polyval вычисляет значения полинома р для каждого элемента х;
- [у.delta] = polyval (p .x.S) или [у,delta] = polyval (p.x.S.mu) – использует структуру S, возвращенную функцией polyfit, и данные о среднем значении (mu(l)) и стандартном отклонении (mu(2)) генеральной совокупности для оценки пр-грешности аппроксимации (y+delta).
Пример:
>> p=[3.0.4.3]; d=polyval(p,[2.6]) d =35 675- polyvalm(p.X) – вычисляет значения полинома для матрицы. Это эквивалентно подстановке матрицы X в полином р. Полином р – вектор, чьи элементы являются коэффициентами полинома в порядке уменьшения степеней, а X – квадратная матрица.
Пример:
>> D=pascal(5) D =1 1 1 1 11 2 3 4 51 3 6 10 151 4 10 20 351 5 15 35 70f=poly(d) f =1.0000-99.0000 626.0000-626.0000 99.0000-1.0000>> polyvalm(f.D) ans =1.0e-006*-0.0003-0.0011-0.0038-0.0059-0.0162-0.0012-0.0048-0.0163-0.0253-0.0692-0.0034-0.0131-0.0447-0.0696-0.1897-0.0076-0.0288-0.0983-0.1529-0.4169-0.0145-0.0551-0.1883-0.2929-0.7984Данный пример иллюстрирует также погрешности численных методов, поскольку точное решение дает нулевую матрицу.
Вычисление производной полинома
Ниже приведена функция, возвращающая производную полинома р:
- polyder(p) – возвращает производную полинома р;
- polyder(a.b) – возвращает производную от произведения полиномов а и b;
- [q,d] = polyder(b.a) – возвращает числитель q и знаменатель d производной от отношения полиномов b/а.
Примеры:
>> a=[3.5.8]:b=[5.3.8]:dp=polyder(a) dp =6 5>> dt=polyder(a,b) dt =60102 158 64>> [q.p]=polyder(b.a) q =1632-16p =9 30 73 80 64