Решение полиномиальных матричных уравнений. Разложение на простые дроби.
Приведенная ниже функция вычисляет собственные значения матричного полинома.
- [Х.е] = polyeig(A0,A1,…Ap) – решает задачу собственных значений для матричного полинома степени р вида:
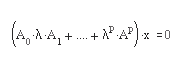
Где степень полинома р – целое неотрицательное число, а А 0, А1 ,…, Аp – входные матрицы порядка n. Выходная матрица X размера nхnр содержит собственные векторы в столбцах. Вектор е размером nр содержит собственные значения.
Пример:
>> A=[1:4:5:8:9:12:13:16] A =1 2 3 45 6 7 89 10 11 121314 15 16>> В=[4:7; 2:5;10:13; 23:26] 34 5 6 72 3 4 510 11 12 1323 24 25 26>> [F.a]=polyeig(A.B) F =0.4373 0.0689 -0.5426 -0.7594-0.3372 -0.4969 0.6675 -0.1314-0.6375 0.7870 0.2927 -0.13140.5374 -0.3591 -0.4176 0.3771a =4.40480.4425-0.3229-1.0000Разложение на простые дроби
Для отношения полиномов b и а используются следующие функции:
- [r,p,k] = residue (b, a) – возвращает вычеты, полюса и многочлен целой части отношения двух полиномов b(s) и a(s) в виде:
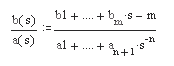
- [b.a] = residue(r.p.k) – выполняет обратную свертку суммы простых дробей (см. более подробное описание в справочной системе) в пару полиномов с коэффициентами в векторах b и а.
Пример:
>> b=[4.3.1]:a=[1.3.7.1]:[r.p,k]=residue(b,a) r=1.9484 + 0.806411.9484-0.806410.1033P =-1.4239 + 2.13051-1.4239-2.13051-0.1523k =[ ] >> [bl,al]=residue(r,p,k) b1=4.0000 3.0000 1.0000a1 =1.0000 3.0000 7.0000 1.0000