Иллюстрированный самоучитель по MatLab

Работа с полиномами. Умножение и деление полиномов.

Полиномы (у нас их принято называть также степенными многочленами) – широко известный объект математических вычислений и обработки данных. Обычно полином записывается в виде:

р(х) = а _n х^n + x _n-1 x^n – 1+… + а ₂ x^2 + а ₁ ^х + а ₀ ,

И так обычно принято в MATLAB для п, отрицательных по умолчанию, хотя и возможны иные формы записи, например:

р(х) = a ₁ x^n + а ₂ x^n-1 +… + а _n х + а _n+1.

Последняя запись обычно принята в MATLAB для n, по умолчанию положительных.

Широкое применение полиномов отчасти обусловлено большими возможностями полиномов в представлении данных, а также их простотой и единообразием вычислений. В этом разделе описаны основные функции для работы с полиномами. При этом полиномы обычно задаются векторами их коэффициентов.

Умножение и деление полиномов

Ниже приведены функции, осуществляющие умножение и деление полиномов, или, что то же самое, свертку двух входных векторов, в которых находятся коэффициенты полиномов, и операцию, обратную свертке.

• w = conv(u.v) – возвращает свертку векторов u и v. Алгебраически свертка – то же самое, что и произведение полиномов, чьи коэффициенты – элементы векторов и и v. Если длина вектора и равна т, а длина вектора v – n, то вектор w имеет длину т+n-1, а его k-й элемент вычисляется по следующей формуле

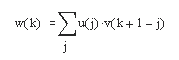
Пример:

• [q,r] = deconv(v.u) – возвращает результат деления полинома v на полином и. Вектор q представляет собой частное от деления, а г – остаток от деления, так что выполняется соотношение v=conv(u,q)+r.

Пример: