Иллюстрированный самоучитель по MatLab

Аппроксимация производных. Аппроксимация Лапласиана.

Для выполнения аппроксимации Лапласиана в MATLAB используется следующая функция:

• del2(11) – возвращает матрицу L дискретной аппроксимации дифференциального оператора Лапласа, примененного к функции U:

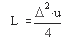
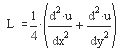
Матрица L имеет тот же размер, что и матрица U, и каждый ее элемент равен разности элемента массива U и среднего значения четырех его соседних элементов (для узлов сетки во внутренней области). Для вычислений используется пятиточечная формула аппроксимации Лапласиана.

Другие формы этой функции также возвращают матрицу L, но допускают дополнительные установки:

• L = del2(U,h) – использует шаг h для установки расстояния между точками в каждом направлении (h – скалярная величина). По умолчанию h=1;
• L = del2(U,hx,hy) – использует hx и hy для точного определения расстояния между точками. Если hx – скалярная величина, то задается расстояние между точками в направлении оси х, если hx – вектор, то он должен иметь размер. равный числу столбцов – матрицы U, и точно определять координаты точек по оси х. Аналогично если hy – скалярная величина, то задается расстояние между точками в направлении оси у, если hy – вектор, то он должен иметь размер. равный числу строк матрицы U, и точно определять координаты точек по оси у:
• L = del2(U,hx.hy,hz….) – если U является многомерным массивом, то расстояния задаются с помощью параметров hx, hy, hz,…. Пример:

На рис. 16.1 представлены графики поверхностей U и V.

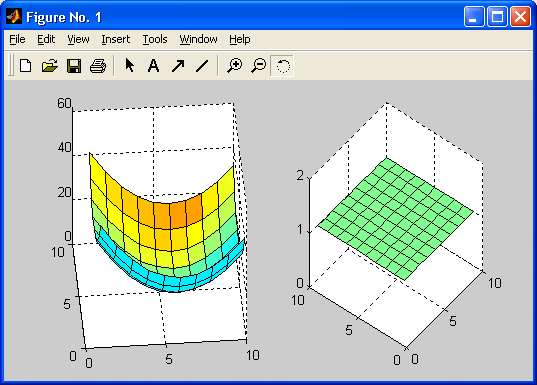
Рис. 16.1. Графики функций U и V