Иллюстрированный самоучитель по Mathematica 5

Число делителей τ(n). Числа с заданным числом делителей.

Это число имеет 3028 цифр! Ага, опять опечатка! А вдруг нет? Ведь мы еще не проверили, что найденное нами число наименьшее.

Пусть n = р^m1, р^m2 …р^mn – каноническое разложение искомого числа, причем в этом разложении простые числа записаны в порядке возрастания. Тогда τ(n) = (m1+1) (m+1)… (m1 + 1).

Так что (m1+l) (m1+l)… (mt+1) = 101x9901. Поскольку о(и) = (mn + 1) (m1+1)… (mt +1) не зависит от чисел pi, а только от показателей m1, m2,…, mt, то наименьшее число и получится тогда, когда мы будем выбирать наименьшие возможные pi, т.е. должно выполняться условие р(= Prime [i]. (Иными словами, мы должны начать с наименьшего простого числа, а затем выбирать их по порядку. Так что pt = 2, 2 = 3 и т.д.) Так как число n – р'р…р' наименьшее, то mi<m2<…mk. (В противном случае мы могли бы уменьшить число, переставив показатели m1 m2…, mk, что совершенно не повлияло бы на количество делителей.) Далее, поскольку (m, + 1)х x(m,+l)… (mt+l) = 101x9901 и все множители в правой части простые, k<2. Если k = 2, то m1 = 2, рr = 3; все возможные варианты в этом случае мы только что исследовали. Если же k= 1, то р, = 2, но зато m = 1000000. Других вариантов в этом случае нет. Но 210СООО° имеет 301030 цифр.

Так что 21000000 > 29900 * 300. Итак, мы доказали, что наименьшим числом, имеющим миллион (не считая самого числа) делителей, является 29900-3ⁿ 10, имеющее 3048 цифр. Как видите, с помощью системы Mathematica мы провели полное исследование математической части сообщения, сделанного Вальтером Литцманом. Что же касается расследования по исторической части сообщения, то здесь я не могу похвастаться особыми успехами. Дело в том, как научный сотрудник, не связанный со спецслужбами, я не смог получить доступ к оригиналам работ Вальтера Литцмана. (Если вы не связаны с этими самыми спецслужбами, то вы хорошо знаете, что сотрудники "самой научной" библиотеки всегда найдут повод отказать вам в выдаче книги, которая, как кажется сотрудникам этих самых служб, может "недостаточно активно" восхвалять существующий строй. А тут зарубежные книги. Тем более популярные. Кто знает, что они там популяризируют?) Поэтому я видел работы Вальтера Литцмана только в переводе. Мне самому приходилось переводить различные книги, и я хорошо знаю, насколько пренебрежительно в некоторых издательствах относятся к словам автора. Особенно в советских. Там больше смотрели как бы чего не вышло, а далеко не за точностью передачи мысли автора и не за отсутствием опечаток в листингах.

Опечатки в вышеупомянутом сообщении я обнаружил еще тогда, когда конструировал системы компьютерной алгебры. Но эти опечатки, конечно, я обнаружил в переводе. Вполне вероятно, что они были сделаны при печати перевода. Но ведь если бы в математическом бюллетене Буэнос-Айреса все было напечатано без опечаток, то почему в Bolletino di Matematica был направлен вопрос? В чем было сомнение? В математических способностях Мерсенна? В энциклопедии Britannica сказано, что Мерсенн действительно публиковал работу "Cogitaeta physico-matematica" и издана она была в Париже в 1644 году. Там же сказано, что он был хорошо знаком с работами Ренэ Декарта, Блеза Паскаля, Галилео Галилея, Христиана Гюйгенса, Пьера Ферма…

В 1635 году Мерсенн основал (частную) Парижскую Академию Наук (Academic Parisienne), которая затем стала Академией Наук Франции… В чем, собственно, было сомнение? В том, что Мерсенн смог найти разложение 1000001 = 101x9901? При его-то энергии? В том, что Мерсенн знал формулу для числа делителей τ(n) = (m+1) (n +1)… (mt +1)? Едва ли, без нее даже подсчитать число делителей было бы весьма трудно. Да и формулу для суммы делителей, очень похожую на формулу для количества делителей, вывели Пьер Ферма и Ренэ Декарт. Причем своими изысканиями в области дружественных чисел Пьер Ферма и Ренэ Декарт занимались независимо, хотя и пришли к тем же формулам, что и один из самых выдающихся арабских математиков абу-Хасан Сабит ибн Корра ибн Марван аль-Харани (836-901). Пьер Ферма сообщил Мерсенну о своем открытии правила Сабита в 1636 году (письмо Мерсенну датировано 24 июня), а Ренэ Декарт – в 1638 году (письмо Мерсенну датировано 31 марта), т.е. за 8 и 6 лет до выхода работы Мерсенна "Cogitaeta physico-matematica". Так что наиболее вероятным мне кажется, что опечатки все же были не только в переводах или в работах Вальтера Литцмана… Если вспомнить, что в средние века в книгах слова печатались подряд, без пробелов, а математическая символика практически отсутствовала, то вполне вероятной выглядит версия об опечатке в показателе степени…

Пример 8.8. График количества делителей.

Теперь давайте построим график количества делителей. Сначала используем функции Table и DivisorSigma для построения таблицы tl (точнее, списка) количества делителей первых n чисел.

Теперь можем использовать функцию ListPlot для построения графика.

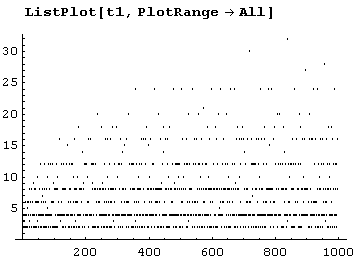
А вот график для n = 100000.

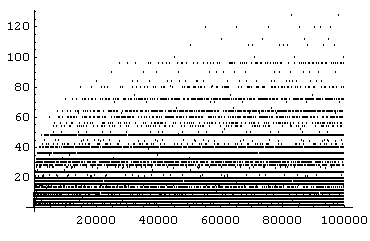
Обратите внимание, несмотря на то что большинство точек расположено весьма невысоко, отдельным точкам удается занять позицию, расположенную выше всех своих предшественников. Абсциссы этих точек являются сверхсоставными числами.