Иллюстрированный самоучитель по Mathematica 5

Недостаточные, избыточные, совершенные и дружественные числа

Рецепт работает! Но как его нашел Вальтер Боро? Он решил искать дружественные пары, в которых оба числа имеют вид Bl-b1-pⁿ -q1 с простыми р, q, и <?, (1= 1, 2). Иными словами, выбираются и фиксируются три числа B1, B2,р,и при каждом n – 1, 2, 3,… ищутся N и N_r. Поскольку В1 и В2 – дружественные числа, то а(В,) = В, + В2 = о(В2), откуда следует, что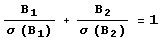

Теперь, вспоминая, что сумма делителей мультипликативна, т.е. а(ху) = а(х)а(у) для взаимно простых х и у, причем:

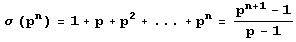
(р – простое), получим:

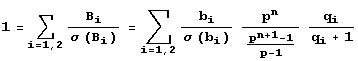
Замечаем, что при n числа n и M, также стремятся к бесконечности. Таким образом, переходя в последнем равенстве к пределу при n › -1, получаем основное уравнение:

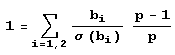
Это соотношение связывает три числа q1,q2 и p, которые следует подставлять в исходную формулу B_i=b_i*pⁿ *q_i. Отыс кивая простейшие решения основного уравнения 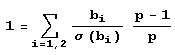, удовлетворяющие условию задачи, мы после некоторых попыток довольно быстро придем к числам B₁= 220, B2= 4и из основного уравнения найдем для р значение 127. Тем самым мы получим ранее наиденную пару B1=220.127² 903223 и B2=4*127² *65032127.

Правда, вначале одно из больших чисел,, и ь все время оказывалось составным. Но второго октября 1972 года Херман те Риле сообшил, что по Формуле приведенной в качестве примера для пары Эйлера А -3-5.11-29-89 -а ы и 5 =34-5-11-2699 = а-5, при я = 19 получаются числа 9|=(<< + 1)Р 1 и а -(<< + 1)(,+1)/-1 по меньшей мере псевдопростые (под псевдопростым числом здесь подразумевается такое число, для которого выполняется сравнение малой теоремы Ферма.

Число А имеет 800 различных делителей, а число В – 3200.

Простым перебором эту пару, конечно, не найти. Система Mathematica позволяет в мгновение ока найти канонические разложения чисел этой пары.

Ну, теперь хоть можете узнать те сомножители, которые эта пара "заимствовала" у пары Эйлера? Без системы Mathematica их бы без усилий не найти!