Основные средства решения дифференциальных уравнений
Решение дифференциальных уравнений второго порядка
Здесь видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ можно задать производную более высокого порядка. Ниже представлено решение двух дифференциальных уравнений второго порядка:
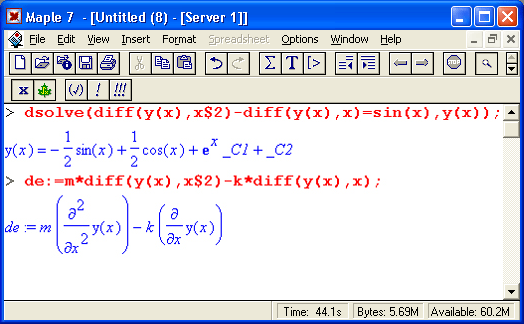
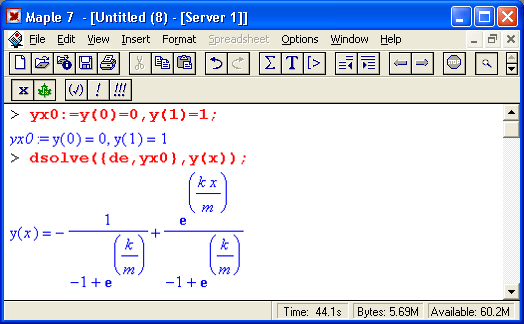
Обратите внимание на решение второго из этих уравнений. Здесь использован прием визуализации исходного дифференциального уравнения, и оно задается значением переменной de. Кроме того, и это особенно важно, решение осуществляется при заданных начальных условиях. Именно поэтому в решении отсутствуют произвольные постоянные вида _СN.
Решение систем дифференциальных уравнений
На рис. 13.1 представлено решение системы из двух дифференциальных уравнений различными методами – в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа. Здесь следует отметить, что решение в виде ряда является приближенным. Поэтому полученные в данном случае аналитические выражения отличаются от явного решения и решения с применением преобразования Лапласа.
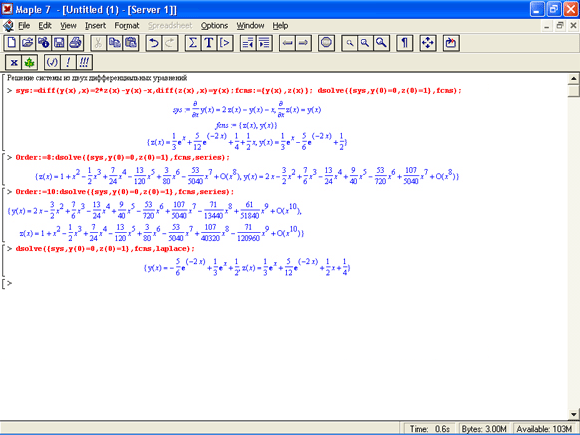
Рис. 13.1. Решение системы из двух дифференциальных уравнений различными методами
Следует отметить, что, несмотря на обширные возможности Maple 7 в области аналитического решения дифференциальных уравнений, оно возможно далеко не всегда. Поэтому, если не удается получить такое решение, полезно попытаться найти решение в численном виде.
