Углубленный анализ дифференциальных уравнений
Задачи углубленного анализа ДУ
Maple 7 существенно доработана по части решения дифференциальных уравнений (ДУ) и систем с ДУ. Эта доработка прежде всего направлена на получение верных решений как можно большего числа ДУ разных классов и систем с ДУ.
В частности, расширен круг нелинейных дифференциальных уравнений, для которых Maple7способна дать аналитические решения.
Весь арсенал средств решения ДУ-и методика их применения вполне заслуживают отражения в отдельной большой книге. Мы ограничимся описанием только трех средств системы Maple 7 – проверки ДУ на автономность, углубленным анализом решения с помощью контроля уровня выхода и получением приближенного полиномиального аналитического решения. Более подробное знакомство с новыми возможностями решения дифференциальных уравнений можно получить из соответствующей статьи справки symbolics в разделе What is new.
Проверка ДУ на автономность
Одиночное дифференциальное уравнение или система дифференциальных уравнений называются автономными, если их правая часть явно не зависит от независимой переменной. Для автономных дифференциальных уравнений или систем при построении графиков решений функцией DEplot не обязательно задавать начальные условия, но нужно указывать диапазон изменения искомых переменных.
Для проверки уравнений (или систем) на автономность используется функция:
autonomous(des,vars,ivar)
Где des – заданное дифференциальное уравнение или (в виде списка) система дифференциальных уравнений; vars – зависимые переменные; ivar – независимая переменная. Если система автономна, то эта функция возвращает true, в противном случае false.
Примеры:
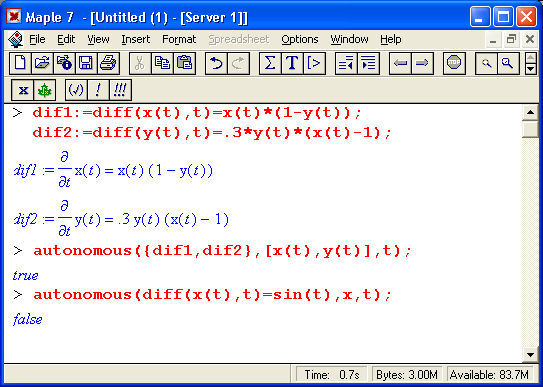
В первом случае система дифференциальных уравнений (модель. Лотки-Вольтерра) автономна, а во втором случае дифференциальное уравнение не автономно.
