Углубленный анализ дифференциальных уравнений
Дадим небольшой комментарий. Нетрудно заметить, что точное аналитическое решение весьма сложно и содержит специальные функции Бесселя и гамма-функции. При порядке полинома 8 (он несколько меньше заданного максимального) решение практически совпадает с точным до значений t < 2, а при максимальном заданном порядке 60 область совпадения расширяется до значений t < 5.5. Затем приближенное решение резко отходит от точного.
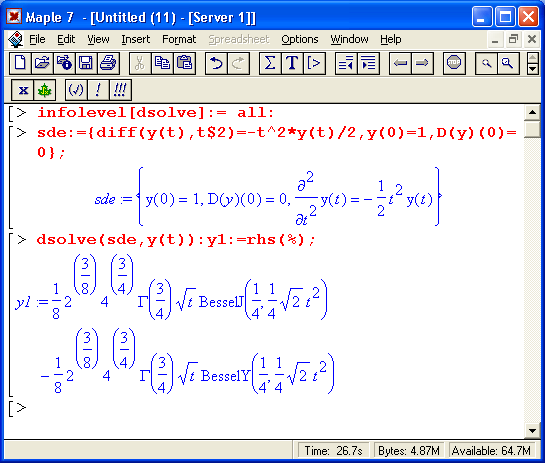
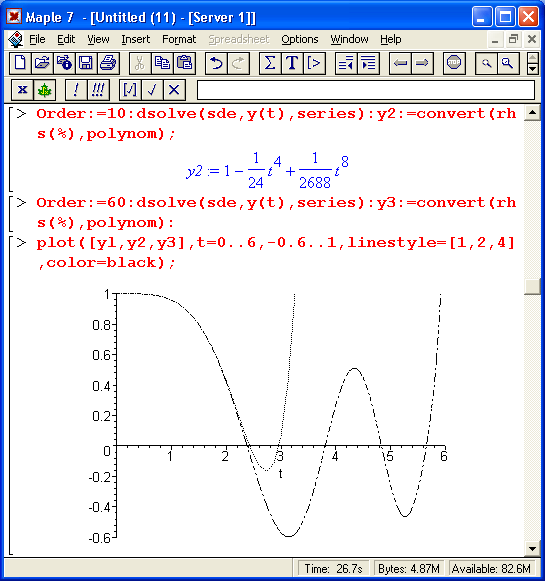
Рис. 13.17. Примеры решения ДУ третьего порядка
Этот пример, с одной стороны, иллюстрирует хорошо известный факт – быстрое нарастание погрешности полиномиального приближения за пределами области хорошего совпадения решений. С другой стороны, он показывает, что степень полинома более 60 (и даже выше) вовсе не так уж бесполезна, как это утверждается во многих статьях и книгах по полиномиальному приближению. Точность полиномиальных вычислений Maple 7 достаточно высока, чтобы обеспечить получение приближенных полиномиальных выражений со степенью порядка десятков и иногда даже сотен. Другое дело, что столь "длинный" полином не всегда удобен для аналитических расчетов, даже несмотря на его структурную простоту.
Что нового мы узнали?
В этим уроке мы научились:
- Использовать основную функцию решения дифференциальных уравнений dsolve.
- Решать дифференциальные уравнения первого порядка.
- Решать дифференциальные уравнения второго порядка.
- Решать системы дифференциальных уравнений,.
- Выполнять численное решение дифференциальных уравнений.
- Решать дифференциальные уравнения с кусочными функциями.
- Использовать структуру неявного представления дифференциальных уравнений DESol
- Применять инструментальный пакет решения дифференциальных уравнений DEtools
- Осуществлять графическое представление решений дифференциальных уравнений.
- Осуществлять углубленный анализ аналитических решений дифференциальных уравнений.
