Численное решение дифференциальных уравнений
Большинство нелинейных дифференциальных уравнений не имеет аналитического решения. Кроме того, часто аналитическое решение и не нужно, но требуется получить ответ в виде графических зависимостей.
В таких случаях для решения дифференциальных уравнений в численном виде используется функция dsolve с параметром numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге-Кутта-Фелберга порядков 4 и 5 (в зависимости от условий адаптации решения к скорости его изменения).
Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Последнее достаточно наглядно иллюстрирует рис. 13.2.
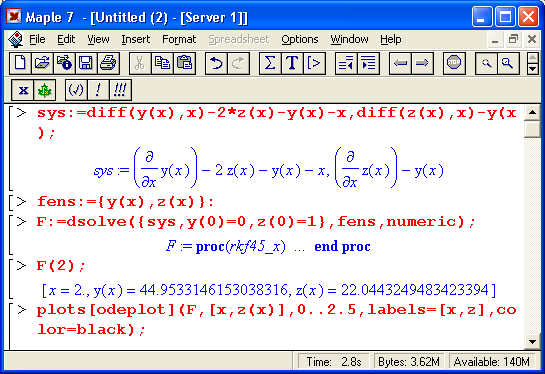
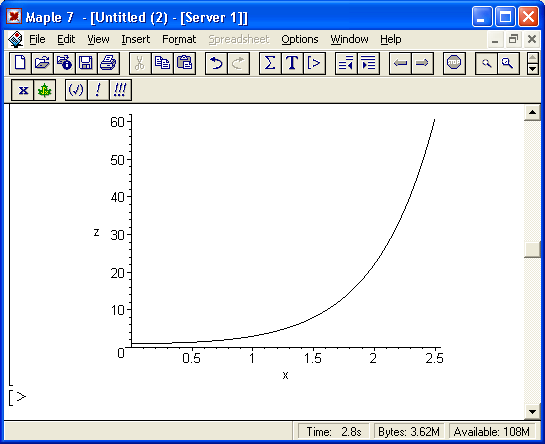
Рис. 13.2. Решение системы дифференциальных уравнений численным методом rkf45 с выводом графика решения
Указанная процедура возвращает особый тип данных, позволяющих найти решение в любой точке или построить график решения (или решений). Для графического отображения Maple 7 предлагает ряд возможностей, и одна из них представлена на рис. 13.2 – см. последнюю строку ввода. При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений дифференциальных уравнений.
В список параметров функции dsolve можно явным образом включить указание на метод решения, например опция mathod=dverk78 задает решение непрерывным методом Рунге-Кутта порядка 7 или 8. Вообще говоря, численное решение дифференциальных уравнений можно производить одним из следующих методов:
- classical – одна из восьми версий классического метода, используемого по умолчанию;
- rkf45 – метод Рунге-Кутта 4 или 5 порядка, модифицированный Фелбергом;
- dverk78 – непрерывный метод Рунге-Кутта порядка 7 или 8;
- gear – одна из двух версий одношагового экстраполяционного метода Гира;
- mgear – одна из трех версий многошагового экстраполяционного метода Гира;
- lsode – одна из восьми версий Ливенморского решателя жестких дифференциальных уравнений;
- taylorseries – метод разложения в ряд Тейлора.
Обилие используемых методов расширяет возможности решения дифференциальных уравнений в численном виде. Большинство пользователей Maple 7 вполне устроит автоматический выбор метода решения по умолчанию. Однако в сложных случаях возможна прямая установка одного из указанных выше методов. С деталями реализации методов можно ознакомиться по справочной системе.
