Графическое представление решений дифференциальных уравнений
Еще интересней вариант графиков, представленный на рис. 13.9. Здесь помимо векторного поля несколько иного стиля построены фазовые портреты решения с использованием функциональной закраски их линий.
Фазовые портреты построены для двух наборов начальных условий: x(0) = y(0) = 1.2 и x(0) = 1 и у(0)=0.7.
Следует отметить, что функция DEplot может обращаться к другим функциям пакета DEtools для обеспечения специальных графических возможностей, таких как построение векторного поля или фазового портрета решения.
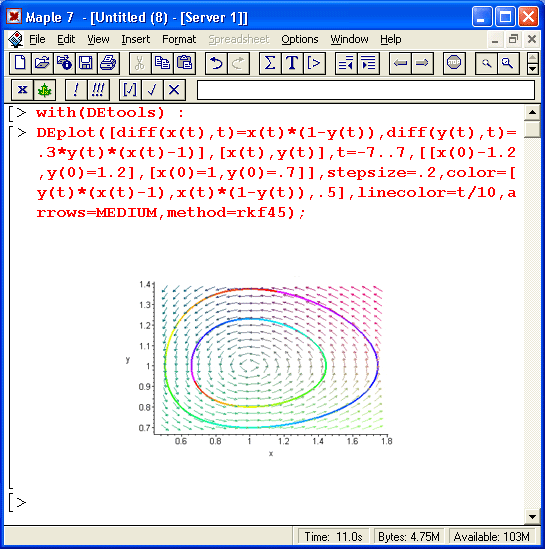
Рис. 13.9. Пример построения двух фазовых портретов на фоне векторного поля
Функция DEplot3d из пакета DEtools
В ряде случаев решение систем дифференциальных уравнений удобно представлять в виде пространственных кривых – например, линий равного уровня или просто в виде кривых в пространстве. Для этого служит функция DEplot3d:
DEplot3d(deqns, vars, trarige, initset, о) DEplot3d(deqns, vars, trang, yrange, xrange, initset, o)
Назначение параметров этой функции аналогично указанному для функции DEplot.
Рисунок 13.10 поясняет применение функции DEPlot3d для решения системы из двух дифференциальных уравнений с выводом фазового портрета колебаний в виде параметрически заданной зависимости x(t), y(t). В данном случае фазовый портрет строится на плоскости по типу построения графиков/линий равной высоты.
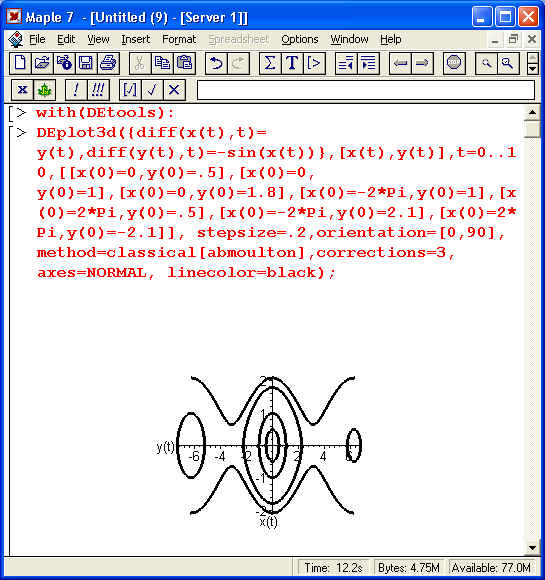
Рис. 13.10. Пример решения системы из двух дифференциальных уравнений с помощью функции DEptot3d
