Графическое представление решений дифференциальных уравнений
В другом примере (рис. 13.6) представлено решение системы из двух нелинейных дифференциальных уравнений. Здесь с помощью функции odeplot строятся графики двух функций – у(х) и z(x).
В этом примере решается система:
у'(х)=z(х), z'(x) = 3 sin(y(x))
При начальных условиях y(0)=0, z(0) = 1 их, меняющемся от -4 до 4 при числе точек решения, равном 25.
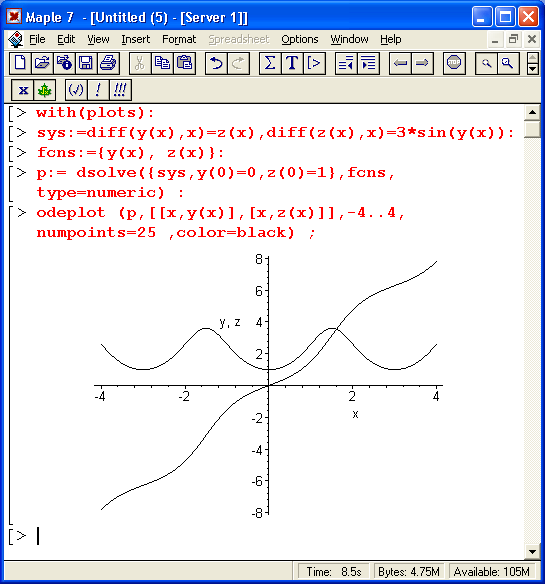
Рис. 13.6. Пример решения системы из двух дифференциальных уравнений
Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета – при этом по осям графика откладываются значения у(х) и z(х) при изменении х в определенных пределах. Рисунок 13.7 демонстрирует построение фазового портрета для системы, представленной выше.
Рис. 13.7. Представление решения системы дифференциальных уравнений в виде фазового портрета
Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок; для построения, поэтому возможность Марle 7 быстро строить фазовые портреты трудно переоценить.
