Графическое представление решений дифференциальных уравнений
Другой пример (рис. 13.11) показывает решение системы из двух дифференциальных уравнений с построением объемного фазового портрета. В этом случае используется трехмерная координатная система и графические построения соответствуют параметрическим зависимостям x(t), y(t) и z(t). Вид фазового портрета напоминает разворачивающуюся в пространстве объемную, спираль.
Функциональная окраска делает график пикантным.
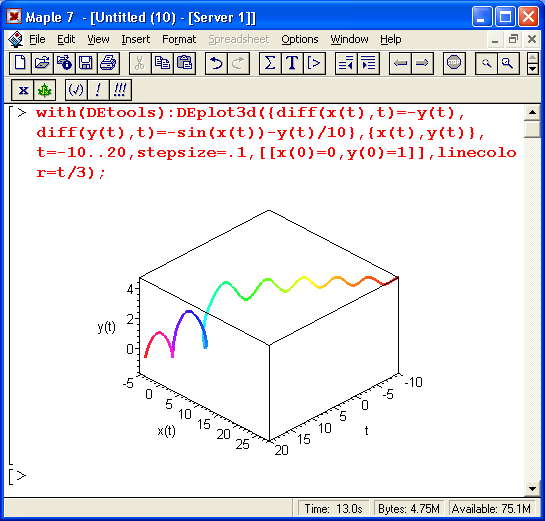
Рис. 13.11. Пример решения системы из двух дифференциальных уравнений с построением трехмерного фазового портрета
Возможности функции DEplot3d позволяют решать системы, состоящие более чем из двух дифференциальных уравнений. Однако в этом случае число решений, представляемых графически, выходит за пределы возможного для трехмерной графики. При этом от пользователя зависит, какие из зависимостей опускаются при построении, а какие строятся.
Функция PDEplot пакета DEtools
Еще одна функция пакета DEtools – DEtools[PDEplot] – служит для построения графиков решения систем с квазилинейными дифференциальными уравнениями первого порядка в частных производных.
Эта функция используется в следующем виде:
PDEplotCpdiffeq, van, i_curve, srange, о) PDEplot(pdiffeq, var, i_curve .srange, xrange, yrange, urange, o)
Здесь помимо упоминавшихся ранее параметров используются следующие: pdiffeq – квазилинейные дифференциальные уравнения первого порядка (PDE), vans – независимая переменная и i_curve – начальные условия для параметрических кривых трехмерной поверхности. Помимо опций, указанных для функции DEplot, здесь могут использоваться следующие опции:
- basechar = TRUE, FALSE. ONLY – устанавливает показ базовых характеристик кривых;
- basecolor, basecolor = b_color – устанавливает цвет базовых характеристик;
- initcolor, initcolor =i_color – инициализация цветов;
- numchar = integer – задает число отрезков кривых, которое не должно быть меньше 4 (по умолчанию 20);
- numsteps = [integerl.integerZ] – задает число шагов интегрирования (по умолчанию [10, 10]).
