Основные функции пакета DEtools
Следует отметить, что подстановки являются мощным средством решения дифференциальных уравнений. Нередки случаи, когда дифференциальное уравнение не решается без их применения.
Дополнительные примеры использования подстановок можно найти в справочной базе данных системы Maple 7.
Функция нормализации ОДУ DEnormal синтаксически записывается в виде:
DEnormal(des,ivar,dvar)
Где des – система дифференциальных уравнений, ivar – независимая переменная и dvar – зависимая переменная.
Применение этой функции поясняют следующие примеры:
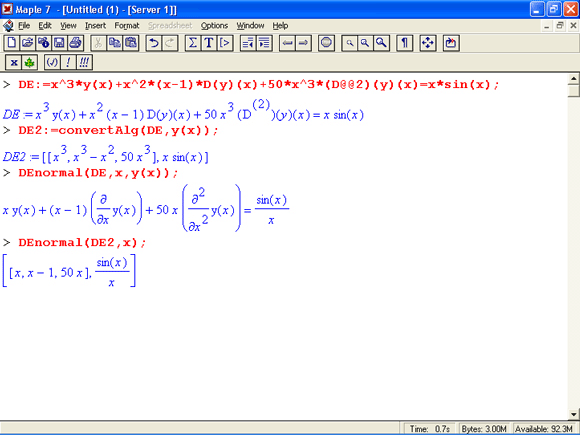
Функция convertAlg(des,dvar) возвращает список коэффициентов формы системы дифференциальных уравнений des с зависимыми переменными dvar.
Это поясняют следующие примеры:
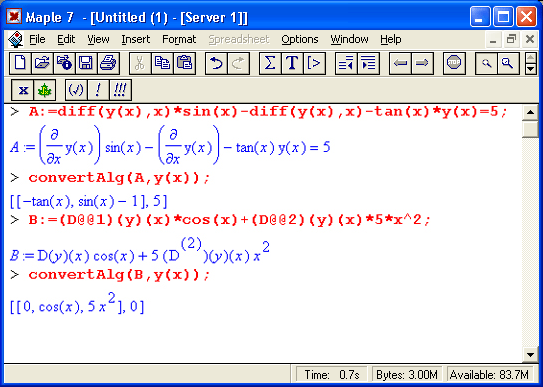
Для изменения переменных в системах дифференциальных уравнений используется функция convertsys:
convertsys(deqns, inits, vars, ivar, yvec, ypvec)
Здесь deqns – одно дифференциальное уравнение или список (множество), представляющие систему дифференциальных уравнений первого порядка, inits – множество или список начальных условий, vans – зависимые переменные, ivar – независимые переменные, yvec – вектор решений и ypvec – вектор производных.
