Интегрирование. Решение уравнений.
Для вычисления неопределенного интеграла от некоторого выражения по определенной переменной выделите в выражении переменную и выполните команду Symbolics › Variable › Integrate (Символика › Переменная › Интегрировать) (рис. 5.14). Вычисленное аналитическое представление неопределенного интеграла появится ниже. При этом результат может содержать как встроенные в Mathcad функции (см. гл. 10 и приложение 3), так и другие спецфункции, которые нельзя непосредственно рассчитать в Mathcad, но символьный процессор "умеет" выдавать их в качестве результата некоторых символьных операций.
Более подробную информацию о символьном решении алгебраических уравнений, дифференцировании и интегрировании (с применением оператора символьного вывода), включая вычисление производных высших порядков, определенных кратных интегралов, можно найти в части III этой книги (см гл 7)
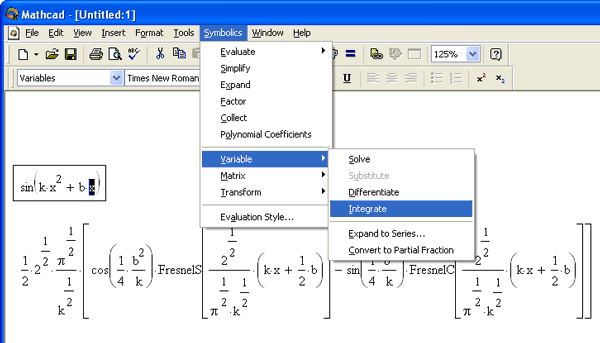
Рис. 5.14. Интегрирование (Integrate) по переменной
Решение уравнений (Solve)
С помощью символьного процессора можно вычислить аналитически значение переменной, при котором выражение обращается в ноль. Для этого:
- Введите выражение.
- Выделите переменную, относительно которой будет решаться уравнение, приравнивающее выражение к нулю.
- Выберите в меню Symbolics (Символика) пункт Variable › Solve (Переменная › Решить) (рис. 5.19).
Подробная информация о символьном решении алгебраических уравнений изложена в части III (см. гл. 8). В частности, там рассказано о возможности решения систем уравнений и задании уравнений в привычной для нас форме логического равенства.
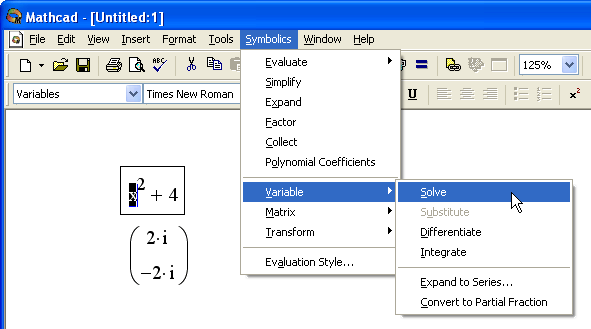
Рис. 5.19. Символьное решение уравнения
