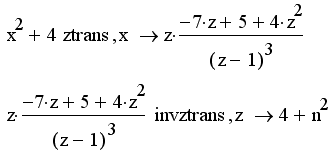Интегральные преобразования
Интегральные преобразования, по определению, ставят в соответствие некоторой функции f (х) другую функцию от другого аргумента F(CO). Причем это соответствие f(x) › F(o)) задается интегральной зависимостью. Символьный процессор Mathcad позволяет осуществлять три вида интегральных преобразований функций – преобразование Фурье, Лапласа и Z-преобразование. Наряду с прямыми преобразованиями, имеется возможность совершать любое из этих трех обратных преобразований, т. е. F (w) › f (x).
Выполняются все символьные интегральные преобразования аналогично уже рассмотренным операциям. Для вычисления преобразования выражения выделяется переменная, по которой будет осуществляться преобразование, и затем выбирается соответствующий пункт меню. Преобразования с применением оператора символьного вывода используются с одним из соответствующих ключевых слов, вслед за которым требуется указать имя нужной переменной.
Приведем примеры символьного расчета каждого из трех интегральных преобразований.
Преобразование Фурье (Fourier)
Преобразование Фурье представляет функцию f (х) в виде интеграла по гармоническим функциям, называемого интегралом Фурье:
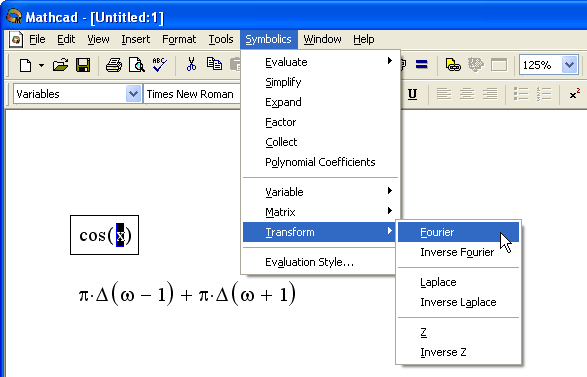
Рис. 5.20. Расчет Фурье-преобразования при помощи меню
Аналитический расчет преобразования Фурье при помощи меню показан на рис. 5.20. В листинге 5.15 приведены два примера вычисления прямого преобразования Фурье с применением ключевого слова fourier и оператора символьного вывода. Листингом 5.16 иллюстрируется обратное преобразование Фурье одной из функций предыдущего листинга.
В Mathcad преобразование Фурье можно вычислить и с помощью численного процессора, использующего популярный алгоритм БПФ (см. разд. "Преобразование Фурье" гл. 14).
Листинг 5.15. Прямое преобразование Фурье:
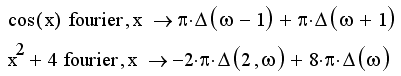
Листинг 5.16. Обратное преобразование:
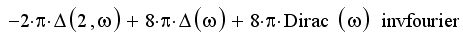
Преобразование Лапласа (Laplace)
Преобразованием Лапласа называют интеграл от f (х) следующего вида:
Рассчитывается преобразование Лапласа совершенно аналогично Фурье-преобразованию (см. предыдущий раздел). Примеры преобразования Лапласа приведены в листинге 5.17.
Листинг 5.17. Прямое и обратное преобразование Лапласа:
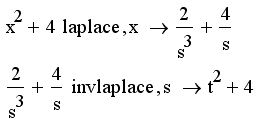
Z-преобразование (Z)
Z-преобразование функции f(x) определяется через бесконечную сумму следующего вида:
Пример Z-преобразования приведен в листинге 5.18.
Листинг 5.18. Прямое и обратное Z-преобразование:
