Эллиптические уравнения
Решение уравнения диффузии тепла при помощи функции relax
Приведем пример применения встроенной функции relax для решения другого уравнения в частных производных (т. е. не уравнения Пуассона, для которого она изначально предназначена). Вычислим при помощи этой функции решение уже хорошо нам знакомого однородного линейного уравнения теплопроводности (см. разд. 13.1.2). Будем использовать явную разностную схему, шаблон которой изображен на рис. 13.6. Для того чтобы "приспособить" для явной схемы функцию relax, требуется только задать ее аргументы в соответствии с коэффициентами, показанными на шаблоне (см. тот же рис. 13.6). Программа, реализующая таким способом явную схему, представлена на листинге 13.8. Число Куранта в этом листинге обозначено переменной с, как и положено явной разностной схеме, она выдает устойчивое решение только для C<1.
Листинг 13.8. Решение уравнения теплопроводности при помощи функции relax:
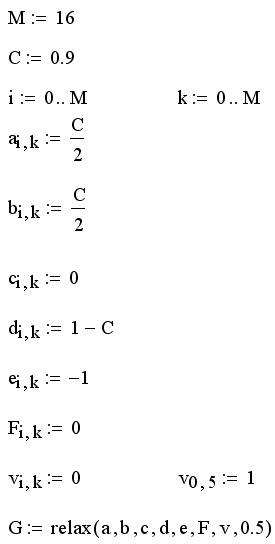
Результат действия программы листинга 13.8 показан на рис. 13.20 в виде трехмерной "поверхности. Если сравнить рис. 13.20 с рис. 13.4, полученным при расчетах по запрограммированной разностной схеме, то в графиках рис. 13.4 нетрудно узнать сечения этой поверхности плоскостями t=const. Еще раз подчеркнем, что использовать встроенную функцию можно только для тех уравнений, которые допускают построение разностной схемы типа "крест" (см. рис. 13.16) или составного фрагмента этой схемы.
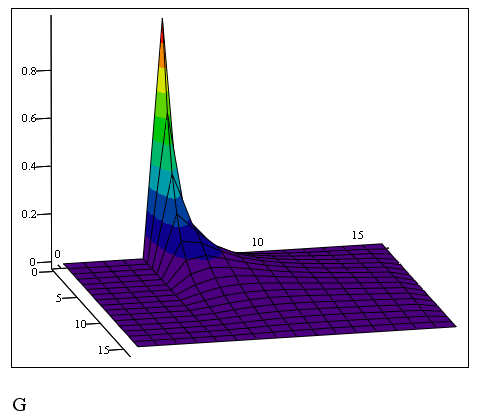
Рис. 13.20. Решение уравнения теплопроводности с помощью функции relax (листинг 13.8)
В заключение разговора об уравнениях в частных производных, нельзя не сказать несколько слов об их визуализации. Результат решения динамических уравнений (зависящих от времени t) выглядит намного эффектнее, если будет представлен в виде анимации. Для создания анимационных роликов расчетное время следует выразить через константу FRAME и затем применить команду View › Animate (Вид › Анимация) (как об этом рассказано в разд. "Создание анимации" гл. 16).
