Равномерное распределение
Самое простое распределение случайной величины – это распределение с постоянной вероятностью. Вероятность p=const=1/ (b-a) при хе(а,b) и P=0, для х вне интервала (а,b). Эту плотность вероятности, наряду с прочими статистическими характеристиками, задают следующие встроенные функции:
- dunif (x,a,b) – плотность вероятности равномерного распределения;
- punif(x,a,b) – функция равномерного распределения;
- qunif(p,a,b) – квантиль равномерного распределения;
- runif (м,а,b) – вектор м независимых случайных чисел, каждое из которых имеет равномерное распределение;
- rnd (x) – случайное число, имеющее равномерную плотность распределения на интервале (о, х);
- х – значение случайной величины;
- Р – значение вероятности;
- (а,b) – интервал, на котором случайная величина распределена равномерно.
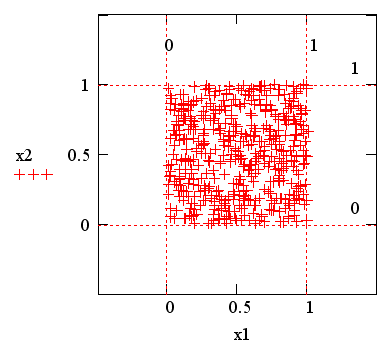
Рис. 14.4. Псевдослучайные числа с равномерным законом распределения
Чаще всего в несложных программах применяется последняя функция, которая приводит к генерации одного псевдослучайного числа. Наличие такой встроенной функции в Mathcad – дань традиции, применяемой в большинстве сред программирования. Пример использования генератора вектора из м случайных чисел показан на рис. 14.4, который получен заменой в двух последних строках листинга 14.7 генератора нормальных чисел на runif (м,0, 1). Плотность вероятности и функция равномерного распределения показаны на рис. 14.5.
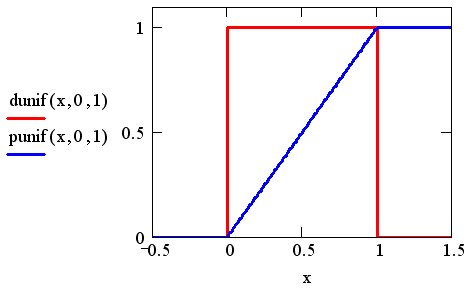
Рис. 14.5. Плотность вероятности и функция равномерного распределения
