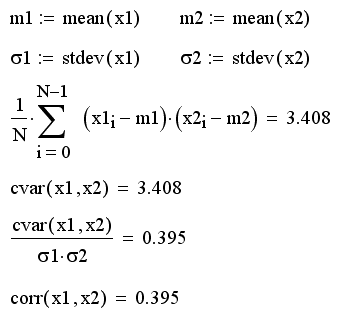Генерация коррелированных случайных чисел. Ковариация и корреляция.
До сих пор мы рассматривали наиболее простой случай применения генераторов независимых случайных чисел. В методах Монте-Карло часто требуется создавать случайные числа с определенной корреляцией.
Приведем пример программы, создающей два вектора x1 и х2 одинакового размера и одним и тем же распределением, случайные элементы которых попарно коррелированы с коэффициентом корреляции R (листинг 14.12).
Листинг 14.12. Генерация попарно коррелированных случайных чисел:
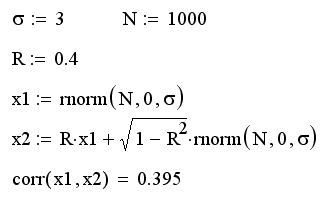
Результат действия программы для R=0.4 показан на рис. 14.13 (слева). Сравните полученную выборку с правым графиком, полученным для высокой корреляции (R=0.9) и с рис. 14.3 (см. разд. 14.1.1) для независимых данных, т. е. R=0.
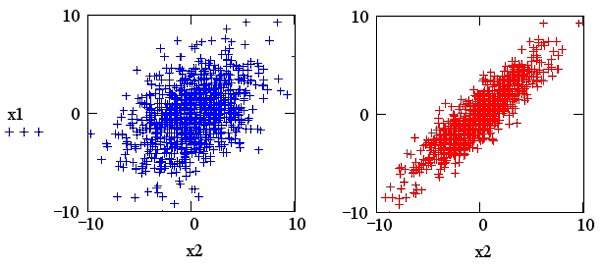
Рис. 14.13. Псевдослучайные числа с корреляцией R=0.4 (листинг 14.12) и R=0.9
Ковариация и корреляция
Функции, устанавливающие связь между парами двух случайных векторов, называются ковариацией и корреляцией (или, по-другому, коэффициентом корреляции). Они различаются нормировкой, как следует из их определения (листинг 14.13).
- согг(х) – коэффициент корреляции двух выборок;
- cvar(x) – ковариация двух выборок;
- x1, х2 – векторы (или матрицы) одинакового размера с выборками случайных данных.
Листинг 14.13. Расчет ковариации и корреляции (продолжение листинга 14.12):