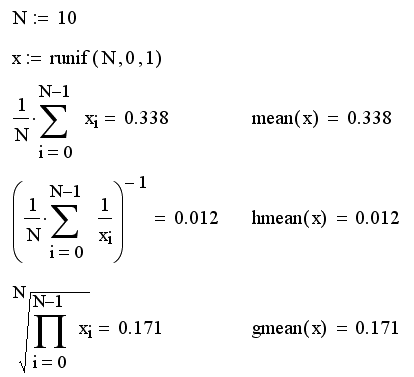Коэффициенты асимметрии и эксцесса. Другие статистические характеристики.
Коэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящий через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическим ожиданием, например нормальным, все нечетные моменты, в том числе и третий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю.
Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной – коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса больше нуля, то распределение имеет более острую вершину, чем распределение Гаусса, если меньше нуля, то более плоскую.
Для расчета коэффициентов асимметрии и эксцесса в Mathcad имеются две встроенные функции.
- kurt(x) – коэффициент эксцесса (kurtosis) выборки случайных данных х;
- skew(x) – коэффициент асимметрии (skewness) выборки случайных данных x.
Примеры расчета коэффициентов асимметрии и эксцесса для распределения Вейбулла (см. рис. 14.10) приведены в листинге 14.14.
Листинг 14.14. Расчет выборочных коэффициентов асимметрии и экспресса:
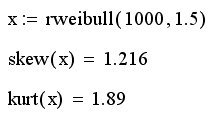
Другие статистические характеристики
В предыдущих разделах были рассмотрены встроенные функции, рассчитывающие наиболее часто используемые статистические характеристики выборок случайных данных. Иногда в статистике встречаются и иные функции, например, помимо арифметического среднего, применяются другие средние значения.
- gmean(x) – геометрическое среднее выборки случайных чисел;
- hmean(x) – гармоническое среднее выборки случайных чисел.
Математическое определение этих функций и пример их использования в Mathcad приведены в листинге 14.15.
Листинг 14.15. Вычисление различных средних значений: