Другие статистические распределения
Как легко заметить по рассмотренным трем распределениям, Mathcad имеет четыре основные категории встроенных функций. Они различаются написанием их первой литеры, а оставшаяся часть имени функций (ниже в списке функций она условно обозначена звездочкой) идентифицирует тот или иной тип распределения.
- d*(x,par) – плотность вероятности;
- р*(х,раг) – функция распределения;
- q*(p,par) – квантиль распределения;
- r* (м,раг) – вектор м независимых случайных чисел, каждое из которых имеет соответствующее распределение;
- х – значение случайной величины (аргумент функции);
- Р – значение вероятности;
- par – список параметров распределения.
Чтобы получить функции, относящиеся, например, к равномерному распределению, вместо * надо поставить unif и ввести соответствующий список параметров par. Он будет состоять в данном случае из двух чисел а,b – интервала распределения случайной величины.
Перечислим все типы распределения, реализованные в Mathcad, вместе с их параметрами, на этот раз обозначив звездочкой * недостающую первую букву встроенных функций. Некоторые из плотностей вероятности показаны на рис. 14.7.
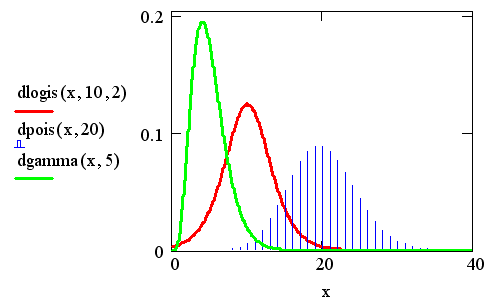
Рис. 14.7. Плотность вероятности некоторых распределений
- *beta(x,s1,s2) – бета-распределение (si,s2>o – параметры, o<x<i).
- *binom(k,n,p) – биномиальное распределение (n – целый параметр, 0<k<n и 0<р<1 – параметр, равный вероятности успеха единичного испытания).
- *cauchy(x,l,s) – распределение Коши (l – параметр разложения, s>0 – параметр масштаба).
- *chisq(x,d) – x2 ("хи-квадрат") распределение (d>0 – число степеней свободы).
- *ехр(х,r) – экспоненциальное распределение (r>0 – показатель экспоненты).
- *F(x,d1,d2) – распределение Фишера (d1,d2>0 – числа степеней свободы).
- *gamma(x,s) – гамма-распределение (s>0 – параметр формы).
- *geom(k,p) – геометрическое распределение (0<р<1 – параметр, равный вероятности успеха единичного испытания).
- *hypergeom(k,a,b,n) – гипергеометрическое распределение (а,b,n – целые параметры).
- *lnоrm(х,m,o) – логарифмически нормальное распределение (m – натуральный логарифм математического ожидания, о>0 – натуральный логарифм среднеквадратичного отклонения).
- *logis(x,l,s) – логистическое распределение (l – математическое ожидание, s>0 – параметр масштаба).
- *nbinom(k,n,p) – отрицательное биномиальное распределение (n>0 – целый параметр, 0<р<1).
- *nоrm(х,m,o) – нормальное распределение (m– среднее значение, o>0 – среднеквадратичное отклонение).
- *pois(k,a) – распределение Пуассона (a>0 – параметр).
- *t(x,d) – распределение Стьюдента (d>0 – число степеней свободы).
- *unif(x,a,b) – равномерное распределение (а<b – границы интервала).
- *weibuli(x,s) – распределение Вейбулла (s>0 – параметр).
Вставку рассмотренных статистических функций в программы удобно осуществлять с помощью диалогового окна Insert Function (Вставка функции). Для этого необходимо выполнить следующие действия:
- Установите курсор на место вставки функции в документе.
- Вызовите диалоговое окно Insert Function нажатием кнопки f(x) на стандартной панели инструментов или командой меню Insert › Function (Вставка › Функция), или нажатием клавиш CTRL + E.
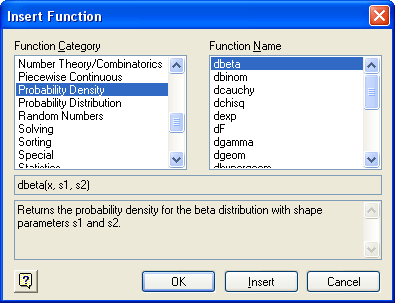
Рис. 14.8. Диалоговое окно Insert Function
- В списке Function Category (Категория функции) (рис. 14.8) выберите одну из категорий статистических функций. Категория Probability Density (Плотность вероятности) содержит встроенные функции для плотности вероятности, Probability Distribution (Функция распределения) – для вставки функций или квантилей распределения, Random Numbers (Случайные числа) – для вставки функции генерации случайных чисел.
- В списке Function Name (Имя функции) выберите функцию, в зависимости от требующегося закона распределения. При выборе того или иного элемента списка в текстовых полях в нижней части окна будет появляться информация о назначении выбранной функции.
- Нажмите кнопку ОК для вставки функции в документ.
