Двухточечные краевые задачи
В следующей строке листинга векторной функции load(x,z) присваиваются левые граничные условия. Эта функция аналогична векторной переменной, определяющей начальные условия для встроенных функций, решающих задачи Коши. Отличие заключается в записи недостающих условий. Вместо конкретных чисел на соответствующих местах пишутся имена искомых элементов вектора z. В нашем случае вместо второго начального условия стоит аргумент z0 функции load. Первый аргумент функции load – это точка, в которой ставится левое граничное условие. Ее конкретное значение определяется непосредственно в списке аргументов функции sbval. Следующая строка листинга определяет правое граничное условие, для введения которого используется функция score(х,у). Оно записывается точно так же, как система уравнений в функции о. Аргумент х функции score аналогичен функции load и нужен для тех случаев, когда граничное условие явно зависит от координаты х. Вектор score должен состоять из такого же числа элементов, что и вектор z.
Реализованный в функции sbval алгоритм стрельбы ищет недостающие начальные условия таким образом, чтобы решение полученной задачи Коши делало функцию score (х, у) как можно ближе к нулю. Как видно из листинга, результат применения sbval для интервала (0.1) присваивается векторной переменной и. Этот вектор похож на вектор z, только в нем содержатся искомые начальные условия вместо приближенных начальных значений, заданных в z. Вектор и содержит, как и z, всего один элемент и0. С его помощью можно определить решение краевой задачи у (х) (последняя строка листинга). Тем самым функция sbval сводит решение краевых задач к задачам Коши. График решения краевой задачи показан на рис. 10.3.
На рис. 10.4 показано решение той же самой краевой задачи, но с другим правым граничным условием, соответствующим R=0, т. е. без зеркала на правой границе. В этом случае слабый обратный пучок света образуется исключительно за счет обратного рассеяния излучения от лазера. Конечно, многие из читателей уже обратили внимание, что реальная физическая среда не может создавать такого большого рассеяния назад. Иными словами, более реальны значения r(х)<<а (х). Однако когда коэффициенты в системе ОДУ при разных yi очень сильно (на порядки) различаются, система ОДУ становится жесткой, и функция sbval не может найти решения, выдавая вместо него сообщение об ошибке "Could not find a solution" (Невозможно найти решение).
Внимание!
Метод стрельбы не годится для решения жестких краевых задач. Поэтому алгоритмы решения жестких ОДУ в Mathcad приходится программировать самому (см. разд. 10.4).
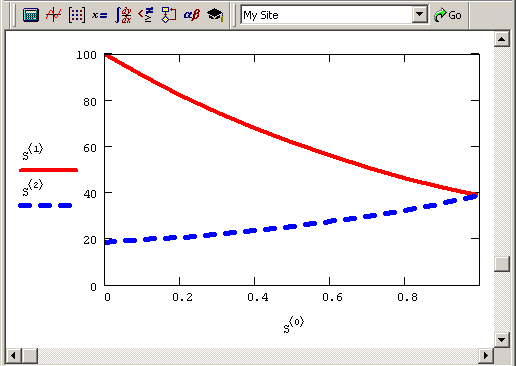
Рис. 10.3. Решение краевой задачи для R=1 (продолжение листинга 10.2)
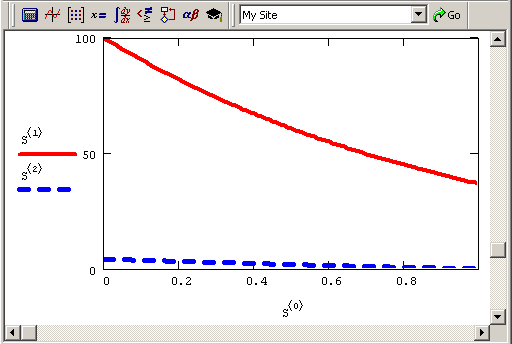
Рис. 10.4. Решение краевой задачи для R=0 (продолжение листинга 10.2 при R=0)
