Решение краевых задач средствами Mathcad. Алгоритм стрельбы.
Для решения краевых задач в Mathcad реализован наиболее популярный алгоритм, называемый методом стрельбы или пристрелки (shooting method). Он, по сути, сводит решение краевой задачи к решению серии задач Коши с различными начальными условиями. Рассмотрим сначала основной принцип алгоритма стрельбы на примере модели световых пучков (см. рис. 10.1), а встроенные функции, реализующие этот алгоритм, приведем в следующем разделе.
Суть метода стрельбы заключается в пробном задании недостающих граничных условий на левой границе интервала и решении затем полученной задачи Коши хорошо известными методами (см. главу 11). В нашем примере не хватает начального условия для y1(0), поэтому сначала зададим ему произвольное значение, например, у1(0)=10. Конечно, такой выбор не совсем случаен, поскольку из физических соображений ясно, что, во-первых, интенсивность излучения – величина заведомо положительная, и, во-вторых, отраженное излучение должно быть намного меньше падающего. Решение задачи Коши с помощью функции rkfixed приведено в листинге 10.1, причем в его последней строке выведены расчетные значения у0 и у1 на правой крайней точке интервала х=1. Разумеется, они не совпадают, т. е. правое краевое условие не выполнено, из чего следует, что полученный результат не является решением поставленной краевой задачи.
Листинг 10.1. Решение пробной задачи Коши для модели (10.1):
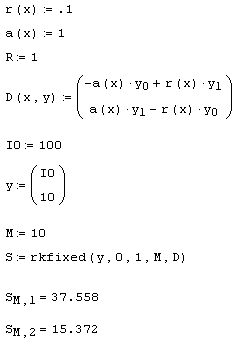
График полученных решений показан на рис. 10.2 (слева). Из него также видно, что взятое наугад второе начальное условие не обеспечило выполнение граничного условия при х=1. В целях лучшего выполнения этого граничного условия следует взять большее значение y1(0), например, y1(0)=15, и вновь решить задачу Коши. Соответствующий результат показан на том же рис. 10.2 (в центре). Граничное условие выполняется с лучшей точностью, но опять-таки оказалось недостаточным. Для еще одного значения y1(0)=20 получается решение, показанное на рис. 10.2 (справа). Из сравнения двух правых графиков легко заключить, что недостающее начальное условие больше 15, но меньше 20. Продолжая подобным образом "пристрелку" по недостающему начальному условию, возможно отыскать правильное решение краевой задачи.
В этом и состоит принцип алгоритма стрельбы. Выбирая пробные начальные условия (проводя пристрелку) и решая соответствующую серию задач Коши, можно найти то решение системы ОДУ, которое (с заданной точностью) удовлетворит граничному условию (или, в общем случае, условиям) на другой границе расчетного интервала.
Конечно, описанный алгоритм несложно запрограммировать самому, оформив его как решение системы заданных алгоритмически уравнений, выражающих граничные условия на второй границе, относительно неизвестных пристрелочных начальных условий. Но делать этого нет необходимости, поскольку он оформлен в Mathcad в виде встроенных функций.
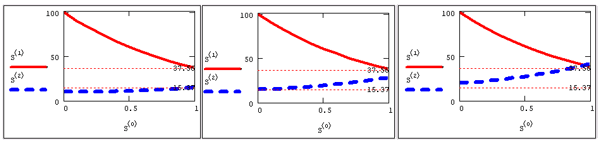
Рис. 10.2. Иллюстрация метода стрельбы (продолжение листинга 10.1)