Краевые задачи с условием во внутренней точке
Для корректного построения графика решения лучше составить его из двух частей – решения задачи Коши на интервале (x0,xf) и другой задачи Коши для интервала (xf,x1). Реализация этого способа приведена в листинге 10.4, который является продолжением листинга 10.3. В последней строке листинга 10.4 выведено значение второй искомой функции на правой границе интервала. Всегда полезно проконтролировать, что оно совпадает с соответствующим пристрелочным параметром (выведенным в последней строке листинга 10.3).
Листинг 10.4. Решение краевой задачи (продолжение листинга 10.3):
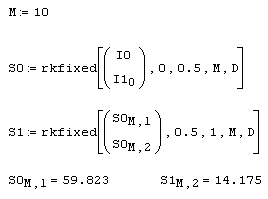
Решение краевой задачи приведено на рис. 10.5. С физической точки зрения естественно, что интенсивность света уменьшается быстрее по мере распространения в более плотной среде в правой половине расчетного интервала. В средней точке xf=0.5, как и ожидалось, производные обоих решений имеют разрыв.
Примечание
Еще один пример решения краевых задач с разрывными коэффициентами ОДУ приведен в справочной системе Mathcad.
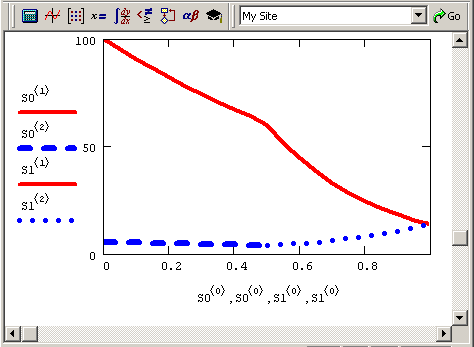
Рис. 10.5. Решение краевой задачи с разрывом в xf=0.5 (продолжение листингов 10.3-10.4)
Ради справедливости необходимо заметить, что разобранную краевую задачу легко решить и с помощью функции sbval, заменив в листинге 10.2 зависимость а (х) на третью строку листинга 10.3. В этом случае листинг 10.2 даст в точности тот же ответ, что показан на рис. 10.5. Однако в определенных случаях (в том числе из соображений быстроты расчетов) удобнее использовать функцию bvaifit, т. е. вести пристрелку с обеих границ интервала.
Совет
Если вы имеете дело с подобными уравнениями, попробуйте сначала решить их как обычную краевую задачу с помощью более надежной и легкой в применении функции sbval.
