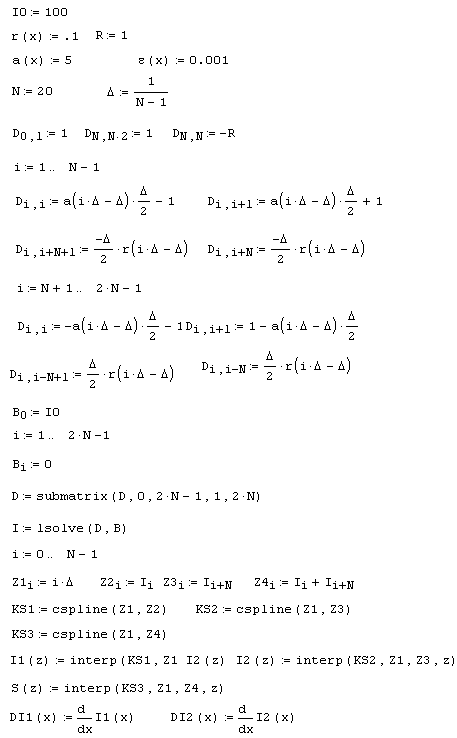Разностные схемы
Решение краевых задач при помощи разностных схем связано с необходимостью разработки собственного алгоритма для каждой конкретной задачи. Как вы помните (см. разд. 10.4), в случае линейных уравнений в результате построения разностной схемы система алгебраических сеточных уравнений также получалась линейной. Это автоматически означало, что она имеет единственное решение, которое в большинстве случаев могло быть найдено стандартными численными методами. В ситуации, когда исходные дифференциальные уравнения нелинейны, система разностных уравнений тоже является нелинейной, и их решение существенно усложняется, хотя бы потому, что оно не является единственным. Поэтому подход к построению разностных схем нелинейных уравнений должен быть специфическим, но наградой за него станет решение задач, с которыми не справляется алгоритм стрельбы (например, жестких).
Подробная разработка алгоритмов и соответствующих программ Mathcad выходит далеко за пределы данной книги, поэтому мы конспективно представим один из приемов решения нелинейных краевых задач, сводящийся к их линеаризации. В общих чертах подход заключается в следующем. Предположим, что некоторое приближение (обозначим его Y(х) и у(х)) к решению нелинейной задачи (10.9) нам известно, и можно считать, что Y › Y+Z и y › y+z, где Z и z – близкие к нулю функции х. Тогда, пользуясь их малостью (по сравнению с Y0 и у0), можно разложить нелинейные слагаемые в уравнениях (10.9) в ряд Тейлора по z и z. Получим:
Y'+Z' = -aY + ry + ε(Y2 + Yy) -aZ + rz + 2εY(Z + z); (10.10)
y'+z' = ay -rY -ε(y2 + Yy) + az -rz -2εy(Z + z).
Теперь, поскольку Y(x) и у(х) являются приближением к решению исходной задачи, то можно считать, что они (приблизительно) удовлетворяют и уравнению, и граничным условиям. Тогда, вычитая (10.9) из (10.10), получим краевую задачу для z (х) и z (х):
Z' = -aZ + rz + 2εY(Z + z);
z' = az -rZ -2εy(Z + z); (10.11)
Z(0) = z(0) = Z(l) = z(l) = 0.
Это и есть та самая новая задача для "маленьких" функций Z (х) и z (х), которую надо решить, и которая, благодаря малости Z и z, является линейной. Вся беда в том, что мы не знаем "больших" функций Y(x) и у(х), а они, увы, входят в задачу (10.11). Тем не менее рецепт получения этих функций напрашивается сам собой: если нелинейность исходных ОДУ не слишком сильная, то в качестве Y и у можно взять решение линейной краевой задачи, т. е. задачи (10.9) с ε(х)=0 (см. разд. 10.4.1).
Сказанное иллюстрируют листинги 10.9 и 10.10, первый из которых решает линейную краевую задачу (являясь, фактически, небольшой модификацией листинга 10.7 из разд. 10.4.2), а второй решает линеаризованную задачу (10.11), учитывая результат листинга 10.9. В листинге 10.9 матрица о и вектор правых частей в являются разностной аппроксимацией ОДУ (ее первые N строк аппроксимируют первое уравнение, а оставшиеся N строк – второе). Такой же смысл и точно такую же структуру имеют матрица с и вектор правых частей с для второй (линеаризованной) задачи (10.11). Для решения сеточных уравнений Dу=B и Cz=G используется (конечно, весьма неэкономично) встроенная функция isolve, реализующая алгоритм Гаусса.
Важно привлечь внимание читателя к последним строкам листинга 10.9. В них осуществляется интерполяция полученного решения системы сеточных уравнений для того, чтобы в нелинейной задаче (в листинге 10.10) можно было использовать непрерывные "большие" функции из линейной задачи. В последней строке листинга 10.10 осуществляется сложение "больших" и "маленьких" функций (результатов листингов 10.9 и 10.10) для получения полного решения нелинейной задачи (10.9), которое изображено на рис. 10.12.
Не будем давать дополнительных комментариев к Mathcad-программам, надеясь, что читатель, заинтересовавшийся нелинейным примером со световыми пучками и эффектом разогрева светом среды, сам разберется в листингах, тем более что техника разработки разностных схем была нами детально разобрана раньше (см. разд. 10.4).
Листинг 10.9. Решение линейной (приближенной) краевой задачи:
