Разностные схемы
Листинг 10.10. Решение линеаризованной задачи (продолжение листинга 10.9):
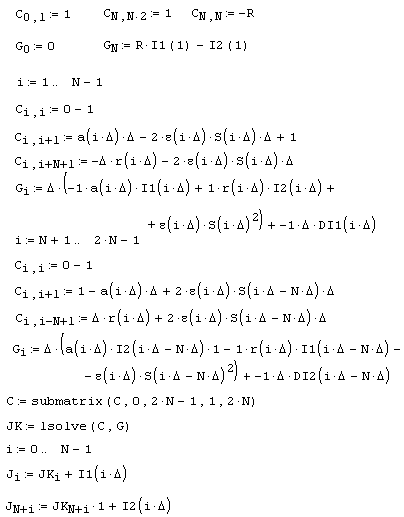
Последний важный момент, который следует обозначить, связан с решением задач, обладающих значительной нелинейностью. Решение, приведенное в листингах 10.9, 10.10 и на рис. 10.12, согласно самой постановке, должно не сильно отличаться от решения линейной краевой задачи, поскольку функции z(x) и z(x) малы по сравнению с Y(x) и у(х). Если же нелинейность сильная, то решение может сильно отличаться от Y и у, и линеаризация (10.11) будет просто неправильной. В этом случае следует слегка усложнить алгоритм решения нелинейной краевой задачи.
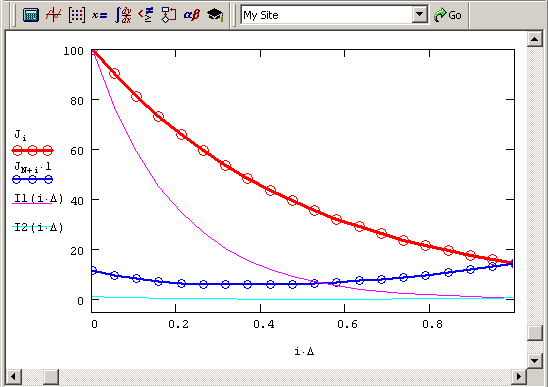
Рис. 10.12. Решение нелинейной краевой задачи разностным методом (продолжение листингов 10.9 и 10.10)
Обозначим полученное в результате решение, как и в листинге 10.10, вектором J(ε), подчеркивая тем самым его зависимость от параметра нелинейности. Очевидно, что J(0) есть решение линейной задачи. Для того чтобы решить задачу с сильной нелинейностью, т. е. довольно большим ε=ε1, можно организовать продолжение по ε как по параметру. Иными словами, используя в качестве начального приближения J (0), можно решить задачу для другого, малого ε=Дε, получив J(Aε), затем, взяв это J(ε) в качестве приближенного решения, получить J(2Aε) и т. д. малыми шагами добраться до желаемого ε1.
Примечание
Упрощенную реализацию этого алгоритма вы найдете на компакт-диске, прилагаемом к книге. Она связана с выводом во внешний файл данных результата задачи из листинга 10.10 и считыванием из него же этих данных в качестве входной информации для следующей итерации. В качестве нулевой итерации используется решение линейной задачи, выводимое предварительно в файл из усовершенствованного листинга 10.9.
