Пример: уравнение диффузии тепла
Линейное и нелинейное уравнения
Если присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа.
- Линейная задача – если коэффициент диффузии о не зависит от температуры и u, кроме того, если источник тепла ф либо также не зависит от u, либо зависит от и линейно. В этом случае неизвестная функция u (x, t) и все ее производные входят в уравнение только в первой степени (линейно).
- Нелинейная задача – если уравнение имеет нелинейную зависимость от u(x,t), т. е. или коэффициент диффузии зависит от u, и (или) источник тепла нелинейно зависит от u.
Решения линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми, и их часто можно получить аналитически (этим проблемам посвящены соответствующие разделы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии.
Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически.
Примечание
Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями D(u) и ф(и). В частности, для металлов в большинстве случаев можно считать, что D=const, в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры.
Обратное уравнение теплопроводности
Замечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с D=const без источников тепла:
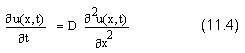
Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает замечательными свойствами.
Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных уравнений (для этого достаточно в листинге 11.1 или 11.2 заменить значение коэффициента диффузии на отрицательное число, например, D=-1), то мы получим заведомо нефизичное решение. Оно показано на рис. 11.5 в виде профилей распределения температуры для нескольких последовательных моментов времени. Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое решение является не проявлением неустойчивости численного алгоритма (как для ситуации, рассмотренной в разд. "Устойчивость"этой главы), а определяется спецификой самой задачи.
Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того, чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение), приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения.
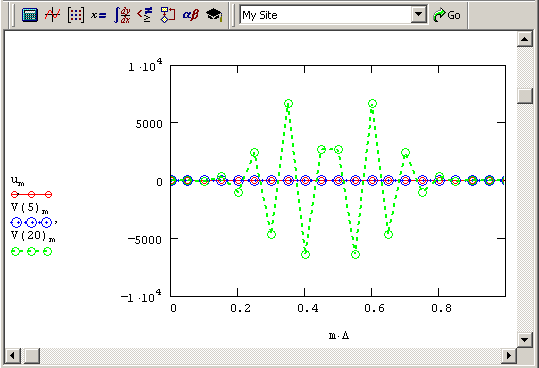
Рис. 11.5. Численное решение обратного уравнения теплопроводности дает совершенно нефизичную картину динамики температуры (см. листинг 11.2 ниже с параметром D=-1)